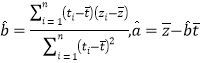题目内容
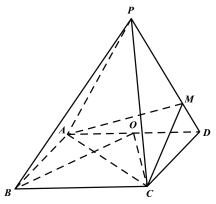
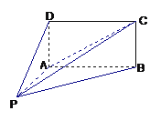
【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() .
.

(I)求证:![]() 平面
平面![]() ;
;
(II)若![]() 为
为![]() 的中点,求
的中点,求![]() 与平面
与平面![]() 所成的角.
所成的角.
【答案】(I)见解析(II)![]() 与平面
与平面![]() 所成的角为
所成的角为![]()
【解析】
试题(I)根据![]() 平面
平面![]() ,证出
,证出![]() ,结合
,结合![]() 1得到
1得到![]() 平面
平面![]() ,从而证出
,从而证出![]() 1.然后在正方形
1.然后在正方形![]() 中证出
中证出![]() ,可得出
,可得出![]() 平面
平面![]() ;
;
(II)设![]() 与
与![]() 相交于点
相交于点![]() ,则点
,则点![]() 是线段
是线段![]() 的中点.连接
的中点.连接![]() ,由题意知
,由题意知![]() 是正三角形.可证
是正三角形.可证![]() 与
与![]() 的交点为重心
的交点为重心![]() ,连接
,连接![]() .
.
由(I)知![]() 平面
平面![]() ,于是
,于是![]() 是
是![]() 与平面
与平面![]() 所成的角.在直角
所成的角.在直角![]() 中.计算
中.计算
![]() 正弦值即可.
正弦值即可.
试题解析:(I)由题意知四边形![]() 是正方形,故
是正方形,故![]() .
.
由![]() 平面
平面![]() ,得
,得![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() ,故
,故![]() .
.
从而得![]() 平面
平面![]() .
.
(II)设![]() 与
与![]() 相交于点
相交于点![]() ,则点
,则点![]() 是线段
是线段![]() 的中点.
的中点.
连接![]() ,由题意知
,由题意知![]() 是正三角形.
是正三角形.
由![]() ,
,![]() 是
是![]() 的中线知:
的中线知:![]() 与
与![]() 的交点为重心
的交点为重心![]() ,连接
,连接![]() .
.
由(I)知![]() 平面
平面![]() ,故
,故![]() 是
是![]() 在平面
在平面![]() 上的射影,于是
上的射影,于是![]() 是
是![]() 与平面
与平面![]() 所成的角.
所成的角.
在直角![]() 中,
中,![]() ,
, ![]() ,
,
所以![]() .
.
故![]() ,即
,即![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
【题目】高一学年结束后,要对某班的50名学生进行文理分班,为了解数学对学生选择文理科是否有影响,有人对该班的分科情况做了如下的数据统计:
理科人数 | 文科人数 | 总计 | |
数学成绩好的人数 | 25 | 30 | |
数学成绩差的人数 | 10 | ||
合计 | 15 |
(Ⅰ)根据数据关系,完成![]() 列联表;
列联表;
(Ⅱ)通过计算判断能否在犯错误的概率不超过![]() 的前提下认为数学对学生选择文理科有影响.
的前提下认为数学对学生选择文理科有影响.
附:![]()
| 0.05 | 0.025 | 0.010 | 0.005 |
| 3.841 | 5.024 | 6.635 | 7.879 |