题目内容
、(本小题满分14分)
已知函数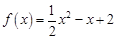 ,数列
,数列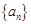 满足递推关系式:
满足递推关系式: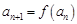 (
(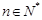 ),且
),且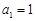 、
、
(Ⅰ)求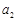 、
、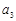 、
、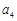 的值;
的值;
(Ⅱ)用数学归纳法证明:当 时,
时,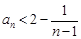 ;
;
(Ⅲ)证明:当 时,有
时,有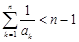 、
、
已知函数
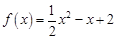 ,数列
,数列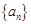 满足递推关系式:
满足递推关系式: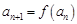 (
(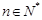 ),且
),且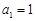 、
、(Ⅰ)求
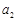 、
、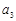 、
、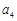 的值;
的值;(Ⅱ)用数学归纳法证明:当
 时,
时,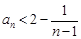 ;
;(Ⅲ)证明:当
 时,有
时,有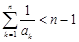 、
、(Ⅰ)【解】由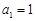 及
及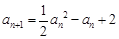 计算得:
计算得: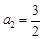 ,
,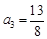 ,
,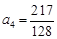 .…3′
.…3′
(Ⅱ)【证】(ⅰ)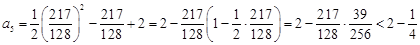
即当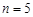 时,结论成立. ……5′
时,结论成立. ……5′
(ⅱ)假设结论对 (
( )成立,即
)成立,即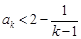 .
.
∵ ,函数
,函数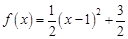 在
在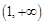 上递增
上递增
∴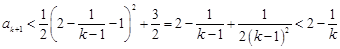 ,即当
,即当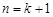 时结论也成立.
时结论也成立.
由(ⅰ)(ⅱ)知,不等式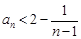 对一切
对一切 都成立. ……9′
都成立. ……9′
(Ⅲ)∵当 时,
时,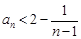 ,∴
,∴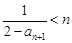 .
.
又由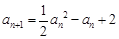 得:
得: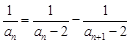 ,且
,且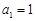 .……11′
.……11′
∴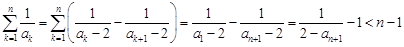 .……14′
.……14′
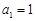 及
及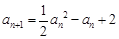 计算得:
计算得: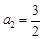 ,
,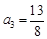 ,
,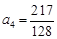 .…3′
.…3′(Ⅱ)【证】(ⅰ)
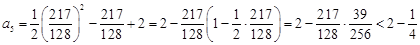
即当
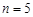 时,结论成立. ……5′
时,结论成立. ……5′(ⅱ)假设结论对
 (
( )成立,即
)成立,即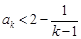 .
.∵
 ,函数
,函数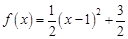 在
在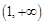 上递增
上递增∴
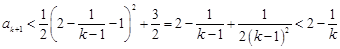 ,即当
,即当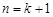 时结论也成立.
时结论也成立.由(ⅰ)(ⅱ)知,不等式
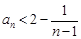 对一切
对一切 都成立. ……9′
都成立. ……9′(Ⅲ)∵当
 时,
时,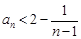 ,∴
,∴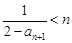 .
.又由
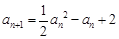 得:
得: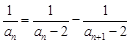 ,且
,且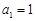 .……11′
.……11′∴
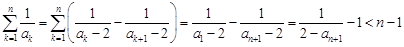 .……14′
.……14′略

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
 的通项公式为
的通项公式为 ,则数列
,则数列 最小项为
最小项为
 最小项为
最小项为
 最小项为
最小项为 最小项为
最小项为 )小题8分)
)小题8分)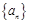 和
和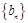 的通项分别为
的通项分别为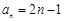 ,
,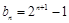 (
(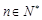 ),集合
),集合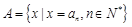 ,
,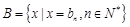 ,设
,设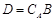 . 将集合
. 将集合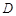 中元素从小到大依次排列,构成数列
中元素从小到大依次排列,构成数列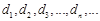 .
.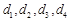 ;
;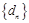 的前
的前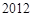 项的和;
项的和;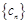 :使得
:使得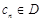 (
(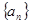 和
和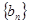 ,若对任意正整数
,若对任意正整数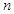 ,恒有
,恒有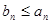 ,则称数列
,则称数列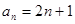 ,请写出一个公比不为1的等比数列
,请写出一个公比不为1的等比数列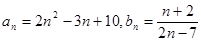 ,求证数列
,求证数列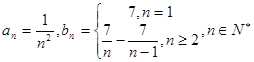 ,构造
,构造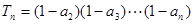 ,
,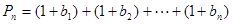 ,求使
,求使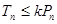 对
对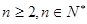 恒成立的
恒成立的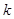 的最小值.
的最小值.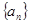 的通项为
的通项为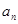 =
=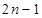 ,
,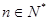 ,其前
,其前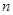 项和为
项和为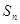 ,则使
,则使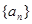 满足
满足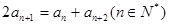 ,它的前
,它的前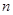 项和为
项和为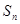 ,且
,且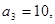
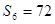 .
.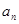 ,
, 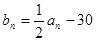 ,求数列
,求数列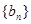 的前
的前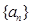 的前n项和为
的前n项和为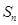 ,若
,若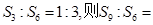 ( )
( )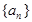 的前
的前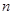 项和
项和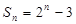 ,则数列
,则数列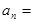

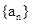 的前n项和满足
的前n项和满足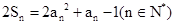
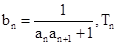 是数列
是数列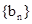 的前n项的和,求证:
的前n项的和,求证: