题目内容
若向量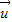 =(3,-6),
=(3,-6),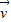 =(4,2),
=(4,2),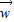 =(-12,-6),则下列结论中错误的是( )
=(-12,-6),则下列结论中错误的是( )A.
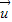 ⊥
⊥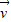
B.
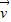 ∥
∥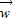
C.
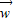 =
=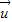 -3
-3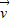
D.对任一向量
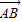 ,存在实数a,b使
,存在实数a,b使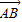 =a
=a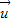 +b
+b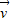
【答案】分析:结合题设条件,利用向量的坐标形式的运算法则,进行判断,能够求出正确结果.
解答:解:∵向量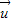 =(3,-6),
=(3,-6),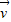 =(4,2),
=(4,2),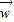 =(-12,-6),
=(-12,-6),
∴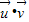 =3×4+(-6)×2=0,
=3×4+(-6)×2=0,
∴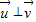 ,故A正确;
,故A正确;
∵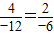 ,
,
∴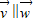 ,故B正确;
,故B正确;
∵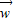 =(-12,-6),
=(-12,-6),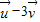 =(-9,-12),
=(-9,-12),
∴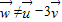 ,故C不正确;
,故C不正确;
∵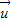 和
和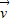 不平行,∴对任一向量
不平行,∴对任一向量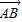 ,存在实数a,b使
,存在实数a,b使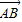 =a
=a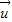 +b
+b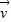 ,
,
故D正确.
故选C.
点评:本题考查平面向量的坐标运算,是基础题.解题时要认真审题,仔细解答.
解答:解:∵向量
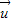 =(3,-6),
=(3,-6),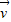 =(4,2),
=(4,2),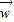 =(-12,-6),
=(-12,-6),∴
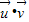 =3×4+(-6)×2=0,
=3×4+(-6)×2=0,∴
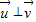 ,故A正确;
,故A正确;∵
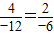 ,
,∴
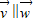 ,故B正确;
,故B正确;∵
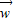 =(-12,-6),
=(-12,-6),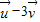 =(-9,-12),
=(-9,-12),∴
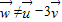 ,故C不正确;
,故C不正确;∵
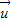 和
和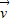 不平行,∴对任一向量
不平行,∴对任一向量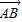 ,存在实数a,b使
,存在实数a,b使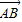 =a
=a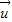 +b
+b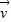 ,
,故D正确.
故选C.
点评:本题考查平面向量的坐标运算,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
若向量
=(3,m),
=(2,-1),
•
=0,则实数m的值为( )
| a |
| b |
| a |
| b |
A、-
| ||
B、
| ||
| C、2 | ||
| D、6 |
若向量
+
=(3,1),
-
=(-1,1),则两向量的夹角是( )
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|