题目内容
数列{an}中,a1=8,a4=2,且满足a n+2-2a n+1+an=0(n∈N *).(1)求数列{an}的通项公式;
(2)设Sn=|a1|+|a2|+…+|an|,求Sn.
解:(1)∵a n+2-2a n+1+an=0,?
∴2a n+1=a n+2+an,
即{an}成等差数列.?
又d=
=-2,
由an=a1+(n-1)d,?
∴an=8-2(n-1)=10-2n.?
(2)由an=10-2n知n≥6时an＜0.?
当n＜6时an≥0,?
Sn=|a1|+|a2|+…+|an|=a1+a2+…+an=
·n=9n-n2.?
当n≥6时,an＜0.?
Sn=|a1|+|a2|+…+|a5|+|a6|+…|an|?
=a1+a2+…+a5-(a6+a7+…+an)?
=2(a1+a2+…+a5)-(a1+a2+…+an)?
=n2-9n+40.?
∴
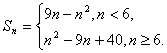
练习册系列答案
相关题目