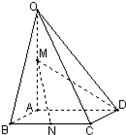
题目内容
如图,在四棱锥O﹣ABCD中,AD∥BC,AB=AD=2BC,OB=OD,M是OD的中点.求证:
(Ⅰ)直线MC∥平面OAB;
(Ⅱ)直线BD⊥直线OA.
(Ⅰ)直线MC∥平面OAB;
(Ⅱ)直线BD⊥直线OA.
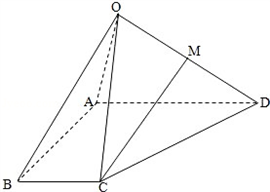
证明:(1)设N是OA的中点,连接MN,NB,
因为M是OD的中点,
所以MN∥AD,且2MN=AD,
又AD∥BC,AD=2BC,
所以MNBC是平行四边形,
所以MC∥NB,
又MC 不在平面OAB上,
NB 平面OAB,
平面OAB,
所以直线MC∥平面OAB;
(2)设H是BD的中点,连接AH,
因为AB=AD,所以AH⊥BD,
又因为OB=OD,所以OH⊥BD
所以BD⊥面OAH
所以BD⊥OA.
因为M是OD的中点,
所以MN∥AD,且2MN=AD,
又AD∥BC,AD=2BC,
所以MNBC是平行四边形,
所以MC∥NB,
又MC 不在平面OAB上,
NB
 平面OAB,
平面OAB,所以直线MC∥平面OAB;
(2)设H是BD的中点,连接AH,
因为AB=AD,所以AH⊥BD,
又因为OB=OD,所以OH⊥BD
所以BD⊥面OAH
所以BD⊥OA.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案
相关题目
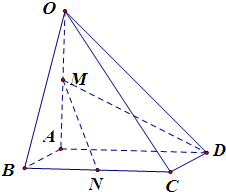 如图,在四棱锥O-ABCD中,底面ABCD是边长为1的正方形,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC中点,以A为原点,建立适当的空间直角坐标系,利用空间向量解答以下问题
如图,在四棱锥O-ABCD中,底面ABCD是边长为1的正方形,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC中点,以A为原点,建立适当的空间直角坐标系,利用空间向量解答以下问题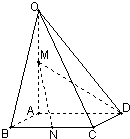 如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,∠ABC=
如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,∠ABC= 如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,
如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形, 如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,
如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,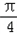 ,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC的中点.
,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC的中点.