题目内容
（1）解不等式x|x-1|-2＜|x-2|；
（2）已知x，y，z均为正数．求证：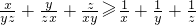
．
解：（1）①当x≥2时，原不等式为x（x-1）-2＜x-2?0＜x＜2．又x≥2，∴x∈∅．
②当1≤x＜2时，原不等式x（x-1）-2＜2-x?-2＜x＜2．又1≤x＜2，∴1≤x＜2．
③当x＜1时，原不等式x（1-x）-2＜2-x?x∈R，又x＜1，∴x＜1．
综上：原不等式的解集为{x|x＜2}．
（2）证明：因为x，y，z均为正数．所以
，
同理可得
，
当且仅当x=y=z时，以上三式等号都成立．
将上述三个不等式两边分别相加，并除以2，得．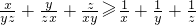
分析：（1）分①当x≥2、当1≤x＜2、当x＜1三种情况，分别求出不等式的解集，再取并集，即得所求．
（2）利用基本不等式证得，同理可得，将上述三个不等式两边分别相加，并除以2，即得要证的不等式．
点评：本题主要考查绝对值不等式的解法，用综合法证明不等式，体现了分类讨论的数学思想，属于中档题．
②当1≤x＜2时，原不等式x（x-1）-2＜2-x?-2＜x＜2．又1≤x＜2，∴1≤x＜2．
③当x＜1时，原不等式x（1-x）-2＜2-x?x∈R，又x＜1，∴x＜1．
综上：原不等式的解集为{x|x＜2}．
（2）证明：因为x，y，z均为正数．所以
，同理可得
，当且仅当x=y=z时，以上三式等号都成立．
将上述三个不等式两边分别相加，并除以2，得
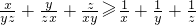．分析：（1）分①当x≥2、当1≤x＜2、当x＜1三种情况，分别求出不等式的解集，再取并集，即得所求．
（2）利用基本不等式证得
，同理可得，将上述三个不等式两边分别相加，并除以2，即得要证的不等式．点评：本题主要考查绝对值不等式的解法，用综合法证明不等式，体现了分类讨论的数学思想，属于中档题．
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目