题目内容
已知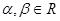 且
且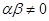 ,数列
,数列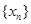 满足
满足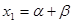 ,
,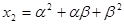 ,
,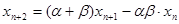 (
(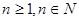 ),令
),令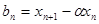 ,
,
⑴求证: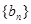 是等比数列;
是等比数列;
⑵求数列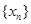 的通项公式;
的通项公式;
⑶若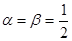 ,求
,求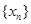 的前
的前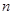 项和
项和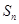 .
.
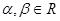 且
且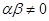 ,数列
,数列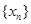 满足
满足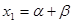 ,
,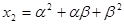 ,
,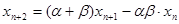 (
(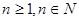 ),令
),令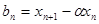 ,
,⑴求证:
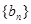 是等比数列;
是等比数列;⑵求数列
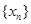 的通项公式;
的通项公式;⑶若
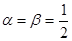 ,求
,求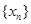 的前
的前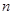 项和
项和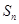 .
.(1)详见解析;(2)当 时,
时, ;当
;当 时,
时, ;
;
(3) .
.
 时,
时, ;当
;当 时,
时, ;
;(3)
 .
.试题分析:(1)根据等比数列的定义,只需证明
 是一个非零常数,∵
是一个非零常数,∵ =
= ,∴
,∴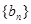 是等比数列;
是等比数列;(2)由(1)可知
 ,联想到
,联想到 是常数),可利用
是常数),可利用 构造等比数列求
构造等比数列求 ,∴两边同时除以
,∴两边同时除以 ,得
,得 ,然后讨论
,然后讨论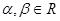 是否相等,当
是否相等,当 时,
时, 是等差数列,解得
是等差数列,解得 ;当
;当 时,
时, 是等比数列,
是等比数列,
(3)当
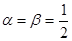 时,
时, ,通项公式是等差数列乘以等比数列,可利用错位相减法求和.
,通项公式是等差数列乘以等比数列,可利用错位相减法求和.试题解析:(1)

 ,∴
,∴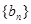 是以
是以 为首项,
为首项, 为公比的等比数列 3分;
为公比的等比数列 3分;(2)由(1)可得
 ,∴
,∴ ,
,
①当
 时,两边同时除以
时,两边同时除以 ,可得
,可得 ,∴
,∴ 是等差数列,
是等差数列,
 6分
6分②当
 时,两边同时除以
时,两边同时除以 ,可得
,可得 ,设
,设 ,
,
 ,
, ,∴
,∴ 是以首项为
是以首项为 ,公比为
,公比为 的等比数列,
的等比数列,

 ,∴
,∴ . 10分
. 10分(3)因为
 ,由⑵可得
,由⑵可得



 14分.
14分.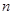 项和.
项和.
练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
 的前
的前 项和为
项和为 ,
, .
. ,求数列
,求数列 的前
的前 .
.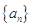 的公差
的公差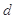 大于0,且
大于0,且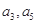 是方程
是方程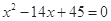 的两根,数列
的两根,数列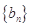 的前
的前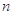 项和为
项和为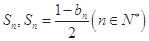 .
.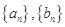 的通项公式;
的通项公式;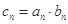 ,求证:
,求证: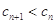 ;
;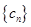 的前
的前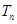 .
. 的首项
的首项 前
前 项和为
项和为 ,且
,且
 是等比数列;
是等比数列; ,求函数
,求函数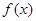 在点
在点 处的导数
处的导数 ,并比较
,并比较 与
与 的大小.
的大小.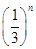 ,则数列{cn}的前n项和Rn=( )
,则数列{cn}的前n项和Rn=( )
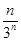
 中,
中, ,则数列
,则数列 的前5项和
的前5项和 = .
= . ,设曲线
,设曲线 在
在 处的切线与
处的切线与 轴交点的纵坐标为
轴交点的纵坐标为 ,则数列
,则数列 的前
的前 中,已知
中,已知
 且
且 ,则前
,则前 项和为
项和为 ,则
,则 的值为__________.
的值为__________.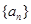 的前
的前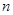 项的和为
项的和为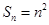 ,则
,则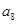 =_________.
=_________.