题目内容
若 的焦点与
的焦点与 的左焦点重合,则
的左焦点重合,则 ( )
( )
| A.-2 | B.2 | C.-4 | D.4 |
C
解析试题分析:
根据题意,由于 ,
, 则左焦点为(-2,0)因此
则左焦点为(-2,0)因此 的焦点为
的焦点为 ,故可知
,故可知
故可知答案为C.
考点:抛物线的性质,椭圆的性质
点评:解决的关键是利用抛物线的焦点坐标来结合对应相等得到p的值,属于基础题。

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
已知双曲线 =1(a>0,b>0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是 ( )
=1(a>0,b>0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是 ( )
| A.[1,2] | B.(1,2) | C.[2,+∞) | D.(2,+∞) |
经过点 ,并且对称轴都在坐标轴上的等轴双曲线的方程为( )
,并且对称轴都在坐标轴上的等轴双曲线的方程为( )
A. | B. |
C. 或 或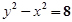 | D. |
椭圆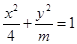 的焦距为2,则
的焦距为2,则 的值为( )
的值为( )
| A.3 | B. | C.3或5 | D.3或 |
抛物线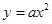 的准线方程为
的准线方程为 ,则实数
,则实数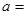 ( )
( )
| A.4 | B.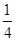 | C.2 | D. |
直线 与曲线
与曲线 相切于点
相切于点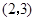 ,则
,则 的值为 ( )
的值为 ( )
| A.5 | B. 6 | C. 4 | D. 9 |
已知函数 与函数
与函数 ,若
,若 与
与 的交点在直线
的交点在直线 的两侧,则实数
的两侧,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
 :抛物线
:抛物线 的准线方程为
的准线方程为 ;命题
;命题 :平面内两条直线的斜率相等是两条直线平行的充分不必要条件;则下列命题是真命题的是( )
:平面内两条直线的斜率相等是两条直线平行的充分不必要条件;则下列命题是真命题的是( )



 的两个焦点分别为
的两个焦点分别为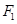 、
、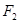 ,若曲线
,若曲线 满足
满足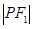 :
: :
: =4:3:2,则曲线
=4:3:2,则曲线


