题目内容
已知函数 与函数
与函数 ,若
,若 与
与 的交点在直线
的交点在直线 的两侧,则实数
的两侧,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
B
解析试题分析:设y=x与f(x)的交点为A和A′,由x= 得:x=±8,所以A和A′的坐标分别是(8,8)和(-8,-8),设f(x)与g(x)的交点为B和B′,此两动点随着g(x)=
得:x=±8,所以A和A′的坐标分别是(8,8)和(-8,-8),设f(x)与g(x)的交点为B和B′,此两动点随着g(x)= 图象上下平移而变动,
图象上下平移而变动,
也就B和B′位置随t值的变化而在双曲线y=
上移动,如图,f(x)与g(x)的交点在直线y=x的两侧,必须B在A的右侧,B′在A′的左侧,
设y=x与g(x)的交点为C和C′,则C和C′的横坐标要在(-8,8)区间内,
也就是方程 =x的解在(-8,8)区间内,由图可知:
=x的解在(-8,8)区间内,由图可知:
当t=6时,f(x)= ,g(x)=
,g(x)=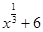 ,y=x,三线共点(8,8);
,y=x,三线共点(8,8);
当t=-6时,f(x)= ,g(x)=
,g(x)= ,y=x,三线共点(-8,-8);
,y=x,三线共点(-8,-8);
所以t的取值范围是(-6,6).故选B.
考点:函数图像的交点问题
点评:本题考查了二元一次不等式表示的平面区域,考查了函数的图象,灵活运用数形结合是解答此题的关键,此题是中档题,也是易错题

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
若 的焦点与
的焦点与 的左焦点重合,则
的左焦点重合,则 ( )
( )
| A.-2 | B.2 | C.-4 | D.4 |
到两互相垂直的异面直线的距离相等的点,在过其中一条直线且平行于另一条直线的平面内的轨迹是( )。
| A.直线 | B.椭圆 | C.抛物线 | D.双曲线 |
如图,用与底面成 角的平面截圆柱得一椭圆截线,则该椭圆的离心率为 ( )
角的平面截圆柱得一椭圆截线,则该椭圆的离心率为 ( )
A. | B. | C. | D.非上述结论 |
已知 是以
是以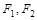 为焦点的椭圆
为焦点的椭圆 上的一点,若
上的一点,若
 ,则此椭圆的离心率为( )
,则此椭圆的离心率为( )
A. | B. | C. | D. |
椭圆 和双曲线
和双曲线 的公共焦点为
的公共焦点为 ,
, 是两曲线的一个交点,那么
是两曲线的一个交点,那么 的值是( )
的值是( )
A. | B. | C. | D. |
已知 是椭圆
是椭圆 的两个焦点,
的两个焦点,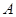 为椭圆上的一点,且
为椭圆上的一点,且 ,则
,则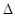
 的面积是( )
的面积是( )
| A.7 | B. | C. | D. |
已知函数 是偶函数,则函数的图象与y轴交点的纵坐标的最大值为:( )
是偶函数,则函数的图象与y轴交点的纵坐标的最大值为:( )
| A.-4 | B.2 | C.3 | D.4 |
 右支上一点,
右支上一点, 分别为双曲线的左、右焦点,I为△
分别为双曲线的左、右焦点,I为△ 的内心,若
的内心,若 成立,则
成立,则 的值为( )
的值为( )


