题目内容
已知正方形的中心为点M(-1,0),一条边所在的直线为l1:3x-y-3=0,求正方形其它三边所在的直线方程.
【答案】分析:先求正方形中心在M(-1,0),到直线3x-y-3=0的距离,然后设出所求直线方程,利用正方形的中心到三边等距离,即可求解.
解答:解:M(-1,0)到直线3x-y-3=0的距离是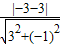 =
=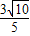 ,
,
所以M到另三边距离也是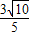 ,其中有一条边和3x-y-3=0平行
,其中有一条边和3x-y-3=0平行
设为3x-y+c=0,由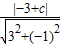 =
=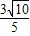 ,解得c=9或c=-3(舍去)
,解得c=9或c=-3(舍去)
故方程为3x-y+9=0
另两条和他们垂直,所以斜率为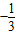
设为:x+3y+b=0,由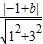 =
=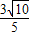 ,解得b=-5或b=7
,解得b=-5或b=7
故所求直线方程为:x+3y-5=0,x+3y+7=0,
故正方形其它三边所在的直线方程为:3x-y+9=0,x+3y-5=0,x+3y+7=0
点评:本题考查点到直线的距离公式,直线的平行和垂直关系,属基础题.
解答:解:M(-1,0)到直线3x-y-3=0的距离是
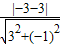 =
=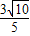 ,
,所以M到另三边距离也是
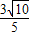 ,其中有一条边和3x-y-3=0平行
,其中有一条边和3x-y-3=0平行设为3x-y+c=0,由
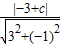 =
=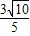 ,解得c=9或c=-3(舍去)
,解得c=9或c=-3(舍去)故方程为3x-y+9=0
另两条和他们垂直,所以斜率为
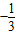
设为:x+3y+b=0,由
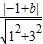 =
=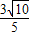 ,解得b=-5或b=7
,解得b=-5或b=7故所求直线方程为:x+3y-5=0,x+3y+7=0,
故正方形其它三边所在的直线方程为:3x-y+9=0,x+3y-5=0,x+3y+7=0
点评:本题考查点到直线的距离公式,直线的平行和垂直关系,属基础题.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
 ,一条边所在的直线的方程是
,一条边所在的直线的方程是 ,求正方形其他三边所在直线的方程.
,求正方形其他三边所在直线的方程.