题目内容
已知圆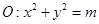
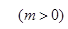 与抛物线
与抛物线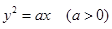 相交于
相交于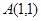 ,
,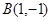 两点
两点
(Ⅰ)求圆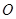 的半径,抛物线的焦点坐标及准线方程;
的半径,抛物线的焦点坐标及准线方程;
(Ⅱ)设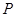 是抛物线上不同于
是抛物线上不同于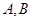 的点,且在圆外部,
的点,且在圆外部,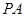 的延长线交圆于点
的延长线交圆于点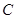 ,直线
,直线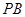 与
与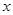 轴交于点
轴交于点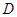 ,点
,点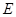 在直线
在直线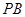 上,且四边形
上,且四边形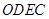 为等腰梯形,求点
为等腰梯形,求点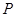 的坐标.
的坐标.
(Ⅰ)圆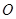 的半径为
的半径为 ,抛物线的焦点坐标
,抛物线的焦点坐标 ,准线方程:
,准线方程: (Ⅱ)
(Ⅱ)
解析试题分析:(Ⅰ)将点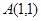 代入圆与抛物线得
代入圆与抛物线得 ,所以圆
,所以圆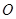 的半径为
的半径为 ,抛物线的焦点坐标
,抛物线的焦点坐标 ,准线方程:
,准线方程:
(Ⅱ)设点 所以PA直线为
所以PA直线为 ,与圆的方程
,与圆的方程 联立得交点C坐标为
联立得交点C坐标为

解得
 ,点
,点
考点:圆抛物线方程及直线与抛物线的位置关系
点评:本题中结合图形可知当四边形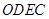 为等腰梯形时直线
为等腰梯形时直线 为两腰,斜率互为相反数,因此首先由已知条件求出点C坐标,得到两直线斜率的关系式
为两腰,斜率互为相反数,因此首先由已知条件求出点C坐标,得到两直线斜率的关系式

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目
 已知抛物线的顶点在坐标原点,对称轴为x轴,焦点F在直线m:y=
已知抛物线的顶点在坐标原点,对称轴为x轴,焦点F在直线m:y=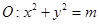
 与抛物线
与抛物线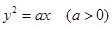 相交于
相交于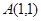 ,
,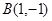 两点
两点
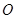 的半径,抛物线的焦点坐标及准线方程;
的半径,抛物线的焦点坐标及准线方程;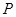 是抛物线上不同于
是抛物线上不同于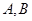 的点,且在圆外部,
的点,且在圆外部,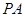 的延长线交圆于点
的延长线交圆于点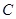 ,直线
,直线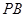 与
与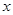 轴交于点
轴交于点 ,点
,点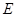 在直线
在直线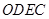 为等腰梯形,求点
为等腰梯形,求点 轴,焦点
轴,焦点 在直线
在直线 上,直线
上,直线 与抛物线相交于
与抛物线相交于 两点,
两点, 为抛物线上一动点(不同于
为抛物线上一动点(不同于 分别交该抛物线的准线
分别交该抛物线的准线 于点
于点 。
。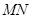 为直径的圆
为直径的圆 经过焦点
经过焦点