题目内容
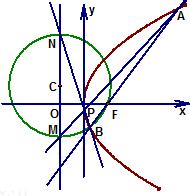 已知抛物线的顶点在坐标原点,对称轴为x轴,焦点F在直线m:y=
已知抛物线的顶点在坐标原点,对称轴为x轴,焦点F在直线m:y=| 4 | 3 |
(1)求抛物线方程;
(2)求证:以MN为直径的圆C经过焦点F,且当P为抛物线的顶点时,圆C与直线m相切.
分析:(1)依题意可知焦点F的坐标,进而求得p,则抛物线的方程可得.
(2)把直线与抛物线方程联立,求得交点A,B的坐标,设出点P的坐标,则直线AP的斜率可表示出来,根据点斜式表示直线AP的方程,把x=-1代入求得M的纵坐标,同理可表示出直线PB的方程把x=-1代入求得N的纵坐标,进而求得
•
=0判断出MF⊥NF,进而可知以MN为直径的圆C经过焦点F.当P为抛物线的顶点时,t=0,可得MN中点,即圆心坐标,进而求得
•
=0,进而可知CF⊥AB,推断出圆C与直线m相切.
(2)把直线与抛物线方程联立,求得交点A,B的坐标,设出点P的坐标,则直线AP的斜率可表示出来,根据点斜式表示直线AP的方程,把x=-1代入求得M的纵坐标,同理可表示出直线PB的方程把x=-1代入求得N的纵坐标,进而求得
| MF |
| NF |
| CF |
| AB |
解答: 解:(1)依题意,焦点F(1,0),抛物线方程为y2=4x.
解:(1)依题意,焦点F(1,0),抛物线方程为y2=4x.
(2)由
得4x2-17x+4=0,x1=4,x2=
,
∴A(4,4),B(
,-1).
设P(
,t),则kPA=
=
,
直线PA:y-4=
(x-4),令x=-1,
得yM=
,即M(-1,
),
同理,直线PB:y+1=
(x-
),令x=-1,得yN=
,
即N(-1,
),
∴
•
=(2,-
)•(2,
)=0,∴MF⊥NF,
∴以MN为直径的圆C经过焦点F.
当P为抛物线的顶点时,t=0,可得MN中点,即圆心C(-1,
),
=(2,-
),
=(-
,-5),
∴
•
=0,即CF⊥AB,
∴圆C与直线m相切.
 解:(1)依题意,焦点F(1,0),抛物线方程为y2=4x.
解:(1)依题意,焦点F(1,0),抛物线方程为y2=4x.(2)由
|
| 1 |
| 4 |
∴A(4,4),B(
| 1 |
| 4 |
设P(
| t2 |
| 4 |
| t-4 | ||
|
| 4 |
| t+4 |
直线PA:y-4=
| 4 |
| t+4 |
得yM=
| 4t-4 |
| t+4 |
| 4t-4 |
| t+4 |
同理,直线PB:y+1=
| 4 |
| t-1 |
| 1 |
| 4 |
| -t-4 |
| t-1 |
即N(-1,
| -t-4 |
| t-1 |
∴
| MF |
| NF |
| 4t-4 |
| t+4 |
| t+4 |
| t-1 |
∴以MN为直径的圆C经过焦点F.
当P为抛物线的顶点时,t=0,可得MN中点,即圆心C(-1,
| 3 |
| 2 |
| CF |
| 3 |
| 2 |
| AB |
| 15 |
| 4 |
∴
| CF |
| AB |
∴圆C与直线m相切.
点评:本题主要考查了直线与圆锥曲线的综合问题.考查了学生运用数学知识分析问题和解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,它们在
,它们在 轴上有共同焦点,抛物线的顶点为坐
轴上有共同焦点,抛物线的顶点为坐