题目内容
(本小题16分)
已知抛物线的顶点在坐标原点,对称轴为 轴,焦点
轴,焦点 在直线
在直线 上,直线
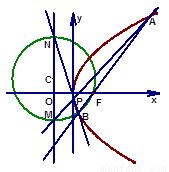
上,直线 与抛物线相交于
与抛物线相交于 两点,
两点, 为抛物线上一动点(不同于
为抛物线上一动点(不同于 ),直线
),直线 分别交该抛物线的准线
分别交该抛物线的准线 于点
于点 。
。
(1)求抛物线方程;
(2)求证:以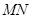 为直径的圆
为直径的圆 经过焦点
经过焦点 ,且当
,且当 为抛物线的顶点时,圆
为抛物线的顶点时,圆 与直线
与直线 相切。
相切。

【答案】
(1)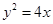
(2)证明见解析
【解析】(1)依题意,焦点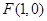 ,抛物线方程为
,抛物线方程为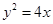 。……………4分
。……………4分
(2)由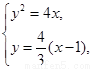 得
得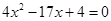 ,
,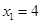 ,
,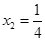 ,
,
∴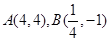 。
……………………6分
。
……………………6分
设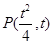 ,则
,则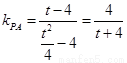 ,
,
直线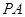 :
: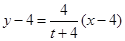 ,令
,令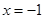 ,
,
得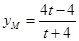 ,即
,即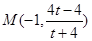 , ……………………8分
, ……………………8分
同理,直线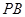 :
: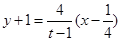 ,令
,令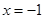 ,得
,得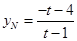 ,
,
即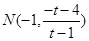 ,……………………10分
,……………………10分
∴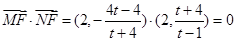 ,∴
,∴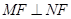 ,
,
∴以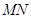 为直径的圆
为直径的圆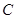 经过焦点
经过焦点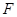 。 ……………………13分
。 ……………………13分
当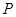 为抛物线的顶点时,
为抛物线的顶点时,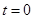 ,可得
,可得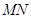 中点,即圆心
中点,即圆心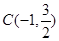 ,
,
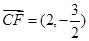 ,
, ,∴
,∴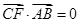 ,即
,即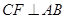 ,
,
∴圆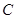 与直线
与直线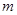 相切。
相切。

练习册系列答案
相关题目
 ,
, ,
, , 点P的横坐标为14,且
, 点P的横坐标为14,且 ,点
,点 是边
是边 上一点,且
上一点,且 .
. 的值与点
的值与点 的坐标;
的坐标; 为线段
为线段 上的一个动点,试求
上的一个动点,试求 的取值范围.
的取值范围.