题目内容
19．在空间中，下列命题正确的是（ ）| A． | 如果直线m∥平面α，直线n?α内，那么m∥n | |
| B． | 如果平面α内的两条直线都平行于平面β，那么平面α∥平面β | |
| C． | 如果平面α外的一条直线m垂直于平面α内的两条相交直线，那么m⊥α | |
| D． | 如果平面α⊥平面β，任取直线m?α，那么必有m⊥β |
分析 利用线面平行、平面与平面平行的判定与性质，线面垂直、平面与平面垂直的判定与性质，即可得出结论．
解答 解：对于A，直线m∥平面α，直线n?α内，则m与n可能平行，可能异面，故不正确；
对于B，如果平面α内的两条相交直线都平行于平面β，那么平面α∥平面β，故不正确；
对于C，根据线面垂直的判定定理可得正确；
对于D，如果平面α⊥平面β，任取直线m?α，那么可能m⊥β，也可能m和β斜交，；
故选：C．
点评 本题主要考查命题的真假判断与应用，考查了空间中直线与平面之间的位置关系、平面与平面之间的位置关系，同时考查了推理能力，属于中档题．
练习册系列答案
相关题目
7．
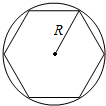如图，半径为R的圆形纸板上有一内接正六边形图案，将一颗豆子随机地扔到平放的纸板上，假设豆子不落在线上，则豆子落在正六边形区域的概率是（ ）
如图，半径为R的圆形纸板上有一内接正六边形图案，将一颗豆子随机地扔到平放的纸板上，假设豆子不落在线上，则豆子落在正六边形区域的概率是（ ）| A． | $\frac{3}{2π}$ | B． | $\frac{3\sqrt{3}}{2π}$ | C． | $\frac{3}{4π}$ | D． | $\frac{3\sqrt{3}}{4π}$ |
4．“m=1”是“直线（m-2）x-3my-1=0与直线（m+2）x+（m-2）y+3=0相互垂直”的（ ）
| A． | 必要而不充分条件 | B． | 充分而不必要条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
11．某市刑警队对警员进行技能测试，测试成绩分为优秀、良好、合格三个等级，测试结果如下表：（单位：人）
若按优秀、良好、合格三个等级分层，从中抽取40人，成绩为良好的有24人，则a等于（ ）
| 优秀 | 良好 | 合格 | |
| 男 | 40 | 105 | 25 |
| 女 | a | 15 | 5 |
| A． | 10 | B． | 15 | C． | 20 | D． | 30 |
8．若p∨q为真命题，则下列结论不可能成立的是（ ）
| A． | p真q真 | B． | p假q真 | C． | p真q假 | D． | p假q假 |
9．下列向量组中，能作为它们所在平面内所有向量的基底的是（ ）
| A． | $\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（0，0） | B． | $\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（-2，-4） | C． | $\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（3，6） | D． | $\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（2，2） |