题目内容
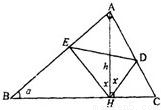
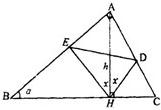 如图∠A=90°,∠B=α,AH=h,α,h为常数,AH⊥BC于H,∠AHE=∠AHD=x,问当x取何值时,△DEH的面积最大?并求出最大面积.
如图∠A=90°,∠B=α,AH=h,α,h为常数,AH⊥BC于H,∠AHE=∠AHD=x,问当x取何值时,△DEH的面积最大?并求出最大面积.
分析:用正弦定理把,△DEH的面积用h,x,α,表示出来,再根据表达式选择方法求最值.本题需要在两三角形△AEH与△ADH中用正弦定理表示出EH与DH两个边.
解答:解:由已知∠EAH=
-α,∠DAH=α,∠HEA=π-x-(
-α)=
+α-x,同理∠ADH=π-α-x
由正弦定理
=
即EH=
同理可得DH=
∴S=
×DH×EHsin2x=
×
×
×sin2x=
×h2×
×sin2x
=
h2×(sin2α-
)
当sin2x=1时,即当x取
时,△DEH的面积最大为
h2×(sin2α-
)
答:当x取
时,△DEH的面积最大为
h2×(sin2α-
)
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
由正弦定理
| h | ||
sin(
|
| EH | ||
sin(
|
| hcosα |
| cos(α-x) |
同理可得DH=
| hsinα |
| sin(α+x) |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| hcosα |
| cos(α-x) |
| hsinα |
| sin(α+x) |
| 1 |
| 2 |
| ||
|
=
| 1 |
| 4 |
| sin 22α |
| sin2α+sin2x |
当sin2x=1时,即当x取
| π |
| 4 |
| 1 |
| 4 |
| sin 22α |
| sin2α+1 |
答:当x取
| π |
| 4 |
| 1 |
| 4 |
| sin 22α |
| sin2α+1 |
点评:本题考查用三角函数的性质求最值,考查了角的变换、正弦定理、三角形的面积公式,本题充分体现了三角函数解题的特点,公式多,变形灵活.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
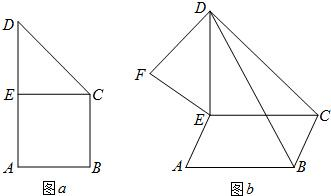 如图a,直角梯形ABCD中,∠A=∠B=90°,AB=BC=
如图a,直角梯形ABCD中,∠A=∠B=90°,AB=BC=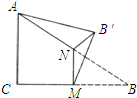 如图∠C=90°,AC=BC,M,N分别为BC和AB的中点,沿直线MN将△BMN折起,使二面角B'-MN-B为60°,则斜线B'A与平面ABC所成角的正切值为
如图∠C=90°,AC=BC,M,N分别为BC和AB的中点,沿直线MN将△BMN折起,使二面角B'-MN-B为60°,则斜线B'A与平面ABC所成角的正切值为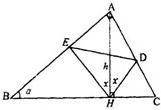 如图∠A=90°,∠B=α,AH=h,α,h为常数,AH⊥BC于H,∠AHE=∠AHD=x,问当x取何值时,△DEH的面积最大?并求出最大面积.
如图∠A=90°,∠B=α,AH=h,α,h为常数,AH⊥BC于H,∠AHE=∠AHD=x,问当x取何值时,△DEH的面积最大?并求出最大面积.