题目内容
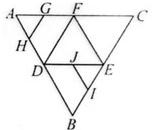
如图∠A=90°,∠B=α,AH=h,α,h为常数,AH⊥BC于H,∠AHE=∠AHD=x,问当x取何值时,△DEH的面积最大?并求出最大面积.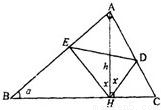
【答案】分析:用正弦定理把,△DEH的面积用h,x,α,表示出来,再根据表达式选择方法求最值.本题需要在两三角形△AEH与△ADH中用正弦定理表示出EH与DH两个边.
解答:解:由已知∠EAH=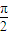 -α,∠DAH=α,∠HEA=π-x-(
-α,∠DAH=α,∠HEA=π-x-( -α)=
-α)=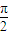 +α-x,同理∠ADH=π-α-x
+α-x,同理∠ADH=π-α-x
由正弦定理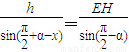 即EH=
即EH=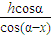
同理可得DH=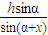
∴S= ×DH×EHsin2x=
×DH×EHsin2x= ×
×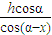 ×
×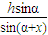 ×sin2x=
×sin2x= ×h2×
×h2×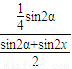 ×sin2x
×sin2x
= h2×(sin2α-
h2×(sin2α-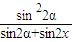 )
)
当sin2x=1时,即当x取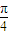 时,△DEH的面积最大为
时,△DEH的面积最大为 h2×(sin2α-
h2×(sin2α-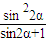 )
)
答:当x取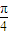 时,△DEH的面积最大为
时,△DEH的面积最大为 h2×(sin2α-
h2×(sin2α-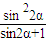 )
)
点评:本题考查用三角函数的性质求最值,考查了角的变换、正弦定理、三角形的面积公式,本题充分体现了三角函数解题的特点,公式多,变形灵活.
解答:解:由已知∠EAH=
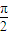 -α,∠DAH=α,∠HEA=π-x-(
-α,∠DAH=α,∠HEA=π-x-( -α)=
-α)=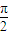 +α-x,同理∠ADH=π-α-x
+α-x,同理∠ADH=π-α-x由正弦定理
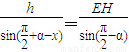 即EH=
即EH=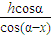
同理可得DH=
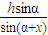
∴S=
 ×DH×EHsin2x=
×DH×EHsin2x= ×
×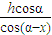 ×
×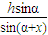 ×sin2x=
×sin2x= ×h2×
×h2×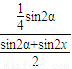 ×sin2x
×sin2x=
 h2×(sin2α-
h2×(sin2α-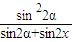 )
)当sin2x=1时,即当x取
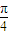 时,△DEH的面积最大为
时,△DEH的面积最大为 h2×(sin2α-
h2×(sin2α-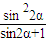 )
)答:当x取
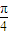 时,△DEH的面积最大为
时,△DEH的面积最大为 h2×(sin2α-
h2×(sin2α-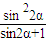 )
)点评:本题考查用三角函数的性质求最值,考查了角的变换、正弦定理、三角形的面积公式,本题充分体现了三角函数解题的特点,公式多,变形灵活.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
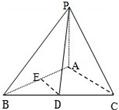 如图,在三棱锥P-ABC中,D、E分别是BC、AB的中点,PA⊥平面ABC,∠BAC=90°,AB≠AC,AC>AD,PC与DE所成的角为α,PD与平面ABC所成的角为β,二面角P-BC-A的平面角为γ,则α,β,γ的大小关系是( )
如图,在三棱锥P-ABC中,D、E分别是BC、AB的中点,PA⊥平面ABC,∠BAC=90°,AB≠AC,AC>AD,PC与DE所成的角为α,PD与平面ABC所成的角为β,二面角P-BC-A的平面角为γ,则α,β,γ的大小关系是( )| A、α<β<γ | B、α<γ<β | C、β<α<γ | D、γ<β<α |
 如图,半径为2的⊙O中,∠AOB=90°,D为OB的中点,AD的延长线交⊙O于点E,则线段DE的长为( )
如图,半径为2的⊙O中,∠AOB=90°,D为OB的中点,AD的延长线交⊙O于点E,则线段DE的长为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 (A)(不等式选讲)不等式log3(|x-4|+|x+5|)>a对于一切x∈R恒成立,则实数a的取值范围是
(A)(不等式选讲)不等式log3(|x-4|+|x+5|)>a对于一切x∈R恒成立,则实数a的取值范围是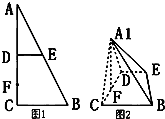 如图1,在Rt△ABC中,∠C=90°,D,E分别是AC,AB上的中点,
如图1,在Rt△ABC中,∠C=90°,D,E分别是AC,AB上的中点,