题目内容
如图,已知圆C:(x-1)2+(y-2)2=2,点P(2,-1),过P点作圆C的切线PA、PB,A、B为切点.
(1)求PA、PB所在直线的方程;
(2)求切线长|PA|;
(3)求∠APB的正弦值;
(4)求AB的方程.
思路解析:求切线可用圆心到直线的距离等于半径;求AB的方程可以设而不求,也可两式相减.
(1)解:设切线的斜率为k.
∵切线过点P(2,-1),∴切线的方程为y+1=k(x-2),
即kx-y-2k-1=0.
又C(1,2),半径r=![]() ,
,
由点到直线的距离公式,得![]() =
=![]() .
.
解之,得k=7或k=-1.
故所求切线PA、PB的方程分别是x+y-1=0和7x-y-15=0.
(2)解:连结AC、PC,则AC⊥AP.
在Rt△APC中,|AC|=![]() ,|PC|=
,|PC|=![]() =
=![]() ,
,
∴|PA|=![]() =
=![]() =2
=2![]() .
.
(3)解:连结CB,则CB⊥BP.
由△APC≌△BPC知,∠APC=∠BPC,
∴∠APB=2∠APC.
∴sin∠APB=sin2∠APC=2sin∠APC·cos∠APC=2×![]() ×
×![]() =
=![]() .
.
(4)解法一:设A(x1,y1)、B(x2,y2),
则(x1-1)2+(y1-2)2=2,(x2-1)2+(y2-2)2=2.
∵CA⊥AP,∴kAC·kAP=-1,即![]() ·
·![]() =-1.
=-1.
∴(y1-2)(y1+1)=-(x1-1)(x1-2).
变形,得(y1-2)(y1-2+3)=-(x1-1)(x1-1-1),
(y1-2)2+(x1-1)2+3(y1-2)-(x1-1)=0.
∵(x1-1)2+(y1-2)2=2,
∴上式可化简为x1-3y1+3=0.
同理可得x2-3y2+3=0.
∵A、B两点的坐标都满足方程x-3y+3=0,
∴直线AB的方程是x-3y+3=0.
解法二:∵∠CAP=∠CBP=90°,
∴A、B两点在以CP为直径的圆上.
∵CP的中点坐标为(![]() ,
,![]() ),即(
),即(![]() ,
,![]() ).
).
又![]() |CP|=
|CP|=![]() ,∴以CP为直径的圆的方程为
,∴以CP为直径的圆的方程为
(x-![]() )2+(y-
)2+(y-![]() )2=(
)2=(![]() )2,即x2+y2-3x-y=0.①
)2,即x2+y2-3x-y=0.①
又圆C:(x-1)2+(y-2)2=2的一般方程为x2+y2-2x-4y+3=0.②
②-①,得x-3y+3=0为直线AB的方程.
深化升华
凡与圆的切线有关的题目,常用切线与过切点的半径垂直这一性质解题.因此,求切线的方程可用点到直线的距离公式;求切线长可用勾股定理;求两切点所在直线的方程,方法有三:一是设而不求法;二是两式相减法;三是求出A、B两点的坐标,应用两点间的距离公式.例题中选择了前两种方法供借鉴.

 星级口算天天练系列答案
星级口算天天练系列答案 (2006•朝阳区二模)如图,已知圆C:(x-1)2+y2=r2(r>1),设M为圆C与x轴负半轴的交点,过M作圆C的弦MN,并使它的中点P恰好落在y轴上.
(2006•朝阳区二模)如图,已知圆C:(x-1)2+y2=r2(r>1),设M为圆C与x轴负半轴的交点,过M作圆C的弦MN,并使它的中点P恰好落在y轴上.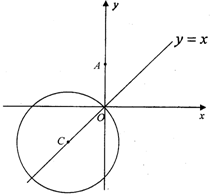 如图,已知圆C:x2+y2+10x+10y=0,点A(0,6).
如图,已知圆C:x2+y2+10x+10y=0,点A(0,6). (2013•潍坊一模)如图,已知圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N(点M必在点N的右侧),且|MN|=3,已知椭圆D:
(2013•潍坊一模)如图,已知圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N(点M必在点N的右侧),且|MN|=3,已知椭圆D: 如图,已知圆C:(x-1)2+y2=r2(r>1),设M为圆C与x轴负半轴的交点,过M作圆C的弦MN,并使它的中点P恰好落在y轴上.
如图,已知圆C:(x-1)2+y2=r2(r>1),设M为圆C与x轴负半轴的交点,过M作圆C的弦MN,并使它的中点P恰好落在y轴上. ,求直线l的斜率的取值范围.
,求直线l的斜率的取值范围.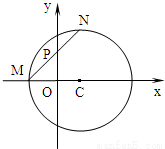 如图,已知圆C:(x-1)2+y2=r2(r>1),设M为圆C与x轴负半轴的交点,过M作圆C的弦MN,并使它的中点P恰好落在y轴上.
如图,已知圆C:(x-1)2+y2=r2(r>1),设M为圆C与x轴负半轴的交点,过M作圆C的弦MN,并使它的中点P恰好落在y轴上. ,求直线l的斜率的取值范围.
,求直线l的斜率的取值范围.