题目内容
 如图,已知圆C:(x-1)2+y2=r2(r>1),设M为圆C与x轴负半轴的交点,过M作圆C的弦MN,并使它的中点P恰好落在y轴上.
如图,已知圆C:(x-1)2+y2=r2(r>1),设M为圆C与x轴负半轴的交点,过M作圆C的弦MN,并使它的中点P恰好落在y轴上.(Ⅰ)当r=2时,求满足条件的P点的坐标;
(Ⅱ)当r∈(1,+∞)时,求点N的轨迹G的方程;
(Ⅲ)过点P(0,2)的直线l与(Ⅱ)中轨迹G相交于两个不同的点E、F,若
 ,求直线l的斜率的取值范围.
,求直线l的斜率的取值范围.
【答案】分析:(1)由已知得,r=2时,可求得M点的坐标为(-1,0),设N(x,y)联立方程可解得MN的中点P坐标;
(2)设N(x,y)由已知得,先利用圆方程求得M点的坐标,再设P(0,b),得:r=b2+1.利用圆的方程与x+1-r=0消去r,即可得出点N的轨迹方程;
(3)设直线l的方程为y=kx+2,将直线的方程代入抛物线的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用向量的数量积公式即可求得k值范围,从而解决问题.
解答:解:(1):由已知得,r=2时,可求得M点的坐标为(-1,0),
设N(x,y)则 解得N(1,±2).
解得N(1,±2).
所以MN的中点P坐标为(0,±1).
(2):设N(x,y)由已知得,在圆方程中令y=0,求得M点的坐标为(1-r,0).
设P(0,b),则由kCPkmp=-1(或用勾股定理)得:r=b2+1.
则 ,消去r,
,消去r,
又r>1,所以点N的轨迹方程为y2=4x(x≠0).
(3)设直线l的方程为y=kx+2,M(x1,x2),N(x2,y2),
消去y得k2x2+(4k-4)x+4=0,因为直线l与抛物线y2=4x(x>0)相交于两个不同的点M,N,
所以△=-32k+16>0,所以 ,
,
又因为 ,所以(x1-1)(x2-1)+y1y2>0,
,所以(x1-1)(x2-1)+y1y2>0,
所以(k2+1)x1x2+(2k-1)(x1+x2)+5>0,得k2+12k>0,
所以k>0或k<-12,
综上可得 .
.
点评:本题是中档题,考查动点的轨迹方程的求法等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.
(2)设N(x,y)由已知得,先利用圆方程求得M点的坐标,再设P(0,b),得:r=b2+1.利用圆的方程与x+1-r=0消去r,即可得出点N的轨迹方程;
(3)设直线l的方程为y=kx+2,将直线的方程代入抛物线的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用向量的数量积公式即可求得k值范围,从而解决问题.
解答:解:(1):由已知得,r=2时,可求得M点的坐标为(-1,0),
设N(x,y)则
 解得N(1,±2).
解得N(1,±2).所以MN的中点P坐标为(0,±1).
(2):设N(x,y)由已知得,在圆方程中令y=0,求得M点的坐标为(1-r,0).
设P(0,b),则由kCPkmp=-1(或用勾股定理)得:r=b2+1.
则
 ,消去r,
,消去r,又r>1,所以点N的轨迹方程为y2=4x(x≠0).
(3)设直线l的方程为y=kx+2,M(x1,x2),N(x2,y2),

消去y得k2x2+(4k-4)x+4=0,因为直线l与抛物线y2=4x(x>0)相交于两个不同的点M,N,
所以△=-32k+16>0,所以
 ,
,又因为
 ,所以(x1-1)(x2-1)+y1y2>0,
,所以(x1-1)(x2-1)+y1y2>0,所以(k2+1)x1x2+(2k-1)(x1+x2)+5>0,得k2+12k>0,
所以k>0或k<-12,
综上可得
 .
.点评:本题是中档题,考查动点的轨迹方程的求法等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
相关题目
 (2006•朝阳区二模)如图,已知圆C:(x-1)2+y2=r2(r>1),设M为圆C与x轴负半轴的交点,过M作圆C的弦MN,并使它的中点P恰好落在y轴上.
(2006•朝阳区二模)如图,已知圆C:(x-1)2+y2=r2(r>1),设M为圆C与x轴负半轴的交点,过M作圆C的弦MN,并使它的中点P恰好落在y轴上.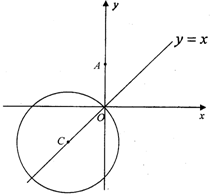 如图,已知圆C:x2+y2+10x+10y=0,点A(0,6).
如图,已知圆C:x2+y2+10x+10y=0,点A(0,6). (2013•潍坊一模)如图,已知圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N(点M必在点N的右侧),且|MN|=3,已知椭圆D:
(2013•潍坊一模)如图,已知圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N(点M必在点N的右侧),且|MN|=3,已知椭圆D: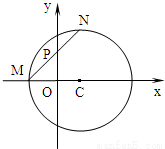 如图,已知圆C:(x-1)2+y2=r2(r>1),设M为圆C与x轴负半轴的交点,过M作圆C的弦MN,并使它的中点P恰好落在y轴上.
如图,已知圆C:(x-1)2+y2=r2(r>1),设M为圆C与x轴负半轴的交点,过M作圆C的弦MN,并使它的中点P恰好落在y轴上.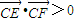 ,求直线l的斜率的取值范围.
,求直线l的斜率的取值范围.