题目内容
椭圆 的右焦点为F,设A(
的右焦点为F,设A(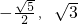 ),P是椭圆上一动点,则|AP|+
),P是椭圆上一动点,则|AP|+ |PF|取得最小值时点P的坐标为
|PF|取得最小值时点P的坐标为
- A.(5,0)
- B.(0,2)
- C.(
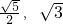 )
) - D.(0,-2)或(0,2)
C
分析:过点P向椭圆右准线做垂线,垂足为D,根据椭圆方程求得离心率和准线方程,进而根据椭圆的第二定义可知|PD|= |PF|,进而可判定当P,A,D三点共线时有最小值,把y=
|PF|,进而可判定当P,A,D三点共线时有最小值,把y= 代入椭圆方程求得答案.
代入椭圆方程求得答案.
解答:过点P向椭圆右准线做垂线,垂足为D,
依题意可知a= ,b=2∴c=1
,b=2∴c=1
∴椭圆离心率e= =
= ,右准线方程为x=
,右准线方程为x= =5
=5
由椭圆的第二定义可知|PD|= =
= |PF|
|PF|
∴|AP|+ |PF|=|AP|+|PD|
|PF|=|AP|+|PD|
当P,A,D三点共线时|AP|+|PD|最小,把y= 代入椭圆方程求得x=
代入椭圆方程求得x= 或-
或- (排除)
(排除)
故选C
点评:本题主要考查了椭圆的应用,考查了学生对椭圆定义和基本知识的理解和应用.
分析:过点P向椭圆右准线做垂线,垂足为D,根据椭圆方程求得离心率和准线方程,进而根据椭圆的第二定义可知|PD|=
 |PF|,进而可判定当P,A,D三点共线时有最小值,把y=
|PF|,进而可判定当P,A,D三点共线时有最小值,把y= 代入椭圆方程求得答案.
代入椭圆方程求得答案.解答:过点P向椭圆右准线做垂线,垂足为D,
依题意可知a=
 ,b=2∴c=1
,b=2∴c=1∴椭圆离心率e=
 =
= ,右准线方程为x=
,右准线方程为x= =5
=5由椭圆的第二定义可知|PD|=
 =
= |PF|
|PF|∴|AP|+
 |PF|=|AP|+|PD|
|PF|=|AP|+|PD|当P,A,D三点共线时|AP|+|PD|最小,把y=
 代入椭圆方程求得x=
代入椭圆方程求得x= 或-
或- (排除)
(排除)故选C
点评:本题主要考查了椭圆的应用,考查了学生对椭圆定义和基本知识的理解和应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
椭圆
+
=1的右焦点为F,设A(-
,
),P是椭圆上一动点,则|AP|+
|PF|取得最小值时点P的坐标为( )
| x2 |
| 5 |
| y2 |
| 4 |
| ||
| 2 |
| 3 |
| 5 |
| A、(5,0) | ||||||
| B、(0,2) | ||||||
C、(
| ||||||
| D、(0,-2)或(0,2) |
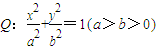 的右焦点为F(c,0),过点F的一动直线m绕点F转动,
的右焦点为F(c,0),过点F的一动直线m绕点F转动,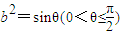 .
.
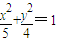 的右焦点为F,设A(
的右焦点为F,设A(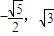 ),P是椭圆上一动点,则|AP|+
),P是椭圆上一动点,则|AP|+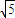 |PF|取得最小值时点P的坐标为( )
|PF|取得最小值时点P的坐标为( ) )
)