题目内容
【题目】![]() 的内角A,B,C的对边分别为a,b,c,已知
的内角A,B,C的对边分别为a,b,c,已知![]()
(1)求角B的大小;
(2)若![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)B=![]()
![]() (2)
(2)![]()
【解析】试题分析:(1)利用正弦定理将已知等式化简,再根据两角和正弦函数公式及变形,求出![]() 的值,结合
的值,结合![]() 为三角形的内角即可算出角
为三角形的内角即可算出角![]() 的大小;(2)三角形内角和定理可求得角
的大小;(2)三角形内角和定理可求得角![]() ,利用正弦定理求出
,利用正弦定理求出![]() 的值,再由三角形的面积公式得到结果.
的值,再由三角形的面积公式得到结果.
试题解析:(1)∵a=bcosC+csinB,∴由正弦定理可得:sinA=sinBcosC+sinCsinB,
∴sin(B+C)=sinBcosC+sinCsinB,即cosBsinC=sinCsinB,∵sinC≠0,∴![]() ,
,
∴![]() ,
, ![]() ,∴B=
,∴B=![]()
(2)由(1)可得![]() ,
,
由正弦定理可得: 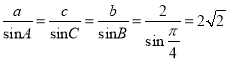 ,∴
,∴![]() ,
,
∴![]()

练习册系列答案
相关题目