题目内容
【题目】如图,四棱锥![]() ,底面
,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() 底面
底面![]() ,
,
![]() 为
为![]() 的中点,
的中点,![]() 为棱
为棱![]() 的中点.
的中点.
(Ⅰ)证明:![]() 平面
平面![]() ;
;
(Ⅱ)已知![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
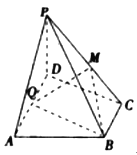
【答案】(I)证明见解析;(Ⅱ) ![]()
【解析】试题分析:(I)连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,可知
,可知![]() 为
为![]() 的中点,利用三角形中位线性质可得
的中点,利用三角形中位线性质可得![]() ∥
∥![]() ,利用直线与平面平行的判定定理可得
,利用直线与平面平行的判定定理可得![]() 平面
平面![]() .(Ⅱ)由(I)可知,
.(Ⅱ)由(I)可知, ![]() ∥平面
∥平面![]() ,所以点
,所以点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离,计算得
的距离,计算得![]() ,
,
![]() ,则点
,则点![]() 到平面
到平面![]() 的距离
的距离 .
.
试题解析:(I)证明连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,因为
,因为![]() ,
, ![]() 为
为![]() 的中点,所以
的中点,所以![]() 为
为![]() 的中点,又
的中点,又![]() 为
为![]() 的中点,故
的中点,故![]() ∥
∥![]() ,又
,又![]() 平面
平面![]() ,所以
,所以![]() ∥平面
∥平面![]() .
.

(II)解由(1)可知, ![]() ∥平面
∥平面![]() ,所以点
,所以点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离,
的距离,
所以![]() ,
,
取![]() 的中点
的中点![]() ,连接
,连接![]() ,所以
,所以![]() ∥
∥![]() ,
, ![]() .
.
又![]() 底面
底面![]() ,所以
,所以![]() 底面
底面![]() .
.
又![]() ,
, ![]() ,所以
,所以![]() ,
,
![]() ,
,
所以![]() ,
,
![]() ,
,
则点![]() 到平面
到平面![]() 的距离
的距离 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某种产品的质量以其指标值来衡量,其指标值越大表明质量越好,且指标值大于或等于102的产品为优质品.现用两种新配方(分别称为![]() 配方和
配方和![]() 配方)做试验,各生产了100件这种产品,并测量了每件产品的指标值,得到了下面的试验结果:
配方)做试验,各生产了100件这种产品,并测量了每件产品的指标值,得到了下面的试验结果:
![]() 配方的频数分布表
配方的频数分布表
指标值分组 |
|
|
|
|
|
频数 | 8 | 20 | 42 | 22 | 8 |
![]() 配方的频数分布表
配方的频数分布表
指标值分组 |
|
|
|
|
|
频数 | 4 | 12 | 42 | 32 | 10 |
(Ⅰ)分别估计用![]() 配方,
配方,![]() 配方生产的产品的优质品率;
配方生产的产品的优质品率;
(Ⅱ)已知用![]() 配方生产的一件产品的利润
配方生产的一件产品的利润![]() (单位:元)与其指标值
(单位:元)与其指标值![]() 的关系式为
的关系式为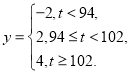
估计用![]() 配方生产的一件产品的利润大于0的概率,并求用
配方生产的一件产品的利润大于0的概率,并求用![]() 配方生产的上述产品平均每件的利润。
配方生产的上述产品平均每件的利润。
【题目】某校高中三个年级共有学生![]() 名,各年级男生、女生的人数如下表:
名,各年级男生、女生的人数如下表:
高一年级 | 高二年级 | 高三年级 | |
男生 |
|
|
|
女生 |
|
|
|
已知在高中学生中随机抽取一名同学时,抽到高三年级女生的概率为![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)现用分层抽样的方法在全校抽取![]() 名学生,则在高二年级应抽取多少名学生?
名学生,则在高二年级应抽取多少名学生?
(Ⅲ)已知![]() ,求高二年级男生比女生多的概率.
,求高二年级男生比女生多的概率.