题目内容
若0<a< ,-
,- <β<0,cos(
<β<0,cos( +α)=
+α)= ,cos(
,cos( -
- )=
)= ,则cos(α+
,则cos(α+ )=
)=
- A.

- B.-

- C.
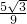
- D.-

C
分析:先利用同角三角函数的基本关系分别求得sin( +α)和sin(
+α)和sin( -
- )的值,进而利用cos(α+
)的值,进而利用cos(α+ )=cos[(
)=cos[( +α)-(
+α)-( -
- )]通过余弦的两角和公式求得答案.
)]通过余弦的两角和公式求得答案.
解答:∵0<a< ,-
,- <β<0,
<β<0,
∴ <
< +α<
+α< ,
, <
< -
- <
<
∴sin( +α)=
+α)= =
= ,sin(
,sin( -
- )=
)= =
=
∴cos(α+ )=cos[(
)=cos[( +α)-(
+α)-( -
- )]=cos(
)]=cos( +α)cos(
+α)cos( -
- )+sin(
)+sin( +α)sin(
+α)sin( -
- )=
)=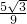
故选C
点评:本题主要考查了三角函数的恒等变换及化简求值.关键是根据cos(α+ )=cos[(
)=cos[( +α)-(
+α)-( -
- )],巧妙利用两角和公式进行求解.
)],巧妙利用两角和公式进行求解.
分析:先利用同角三角函数的基本关系分别求得sin(
 +α)和sin(
+α)和sin( -
- )的值,进而利用cos(α+
)的值,进而利用cos(α+ )=cos[(
)=cos[( +α)-(
+α)-( -
- )]通过余弦的两角和公式求得答案.
)]通过余弦的两角和公式求得答案.解答:∵0<a<
 ,-
,- <β<0,
<β<0,∴
 <
< +α<
+α< ,
, <
< -
- <
<
∴sin(
 +α)=
+α)= =
= ,sin(
,sin( -
- )=
)= =
=
∴cos(α+
 )=cos[(
)=cos[( +α)-(
+α)-( -
- )]=cos(
)]=cos( +α)cos(
+α)cos( -
- )+sin(
)+sin( +α)sin(
+α)sin( -
- )=
)=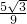
故选C
点评:本题主要考查了三角函数的恒等变换及化简求值.关键是根据cos(α+
 )=cos[(
)=cos[( +α)-(
+α)-( -
- )],巧妙利用两角和公式进行求解.
)],巧妙利用两角和公式进行求解. 
练习册系列答案
相关题目
若0<a<1,且函数f(x)=|logax|,则下列各式中成立的是( )
A、f(2)>f(
| ||||
B、f(
| ||||
C、f(
| ||||
D、f(
|