题目内容
给出下列四个命题
①命题“?x∈R,cosx>0”的否定是“?x∈R,cosx≤0”;
②若0<a<1,则f(x)=x2+ax-3只有一个零点;
③若lga+lgb=lg(a+b),则a+b的最小值为4;
④对于任意实数x,有f(-x)=f(x),且当x>0时,f'(x)>0,则当x<0时,f'(x)<0.
其中正确的命题有
①命题“?x∈R,cosx>0”的否定是“?x∈R,cosx≤0”;
②若0<a<1,则f(x)=x2+ax-3只有一个零点;
③若lga+lgb=lg(a+b),则a+b的最小值为4;
④对于任意实数x,有f(-x)=f(x),且当x>0时,f'(x)>0,则当x<0时,f'(x)<0.
其中正确的命题有
①③④
①③④
(填所有正确的序号)分析:①命题“?x∈R,cosx>0”的否定是“?x∈R,cosx≤0”;可由全称命题的否定的书写规则判断其真假;
②若0<a<1,则f(x)=x2+ax-3只有一个零点;可由函数的图象特征进行判断;
③若lga+lgb=lg(a+b),则a+b的最小值为4;可由基本不等式将方程转化关于a+b不等式,再解不等式求出a+b的最小值,进行验证;
④对于任意实数x,有f(-x)=f(x),且当x>0时,f'(x)>0,则当x<0时,f'(x)<0,此命题的真假可由函数的单调性与导数的关系以及函数的单调性与偶函数的关系进行判断.
②若0<a<1,则f(x)=x2+ax-3只有一个零点;可由函数的图象特征进行判断;
③若lga+lgb=lg(a+b),则a+b的最小值为4;可由基本不等式将方程转化关于a+b不等式,再解不等式求出a+b的最小值,进行验证;
④对于任意实数x,有f(-x)=f(x),且当x>0时,f'(x)>0,则当x<0时,f'(x)<0,此命题的真假可由函数的单调性与导数的关系以及函数的单调性与偶函数的关系进行判断.
解答:解:①命题“?x∈R,cosx>0”的否定是“?x∈R,cosx≤0”是一个真命题,由于原命题是一个全称命题,故其否定是一个特称命题;
②若0<a<1,则f(x)=x2+ax-3只有一个零点是个假命题,由于x=0时,f(0)<0,x趋向于负无穷大与正无穷大时函数值都是正数,故此函数至少有两个零点;
③若lga+lgb=lg(a+b),则a+b的最小值为4是个真命题,由lga+lgb=lg(a+b),得ab=a+b≤(
)2解得a+b≥4,故a+b的最小值为4;
④对于任意实数x,有f(-x)=f(x),且当x>0时,f'(x)>0,则当x<0时,f'(x)<0,是个真命题,由对于任意实数x,有f(-x)=f(x),知此函数是一个偶函数,x>0时,f'(x)>0,知函数在(0,+∞)上是增函数,故在(-∞,0)上是减函数,所以有x<0时,f'(x)<0,
综上证明知①③④是真命题
故答案为:①③④
②若0<a<1,则f(x)=x2+ax-3只有一个零点是个假命题,由于x=0时,f(0)<0,x趋向于负无穷大与正无穷大时函数值都是正数,故此函数至少有两个零点;
③若lga+lgb=lg(a+b),则a+b的最小值为4是个真命题,由lga+lgb=lg(a+b),得ab=a+b≤(
| a+b |
| 2 |
④对于任意实数x,有f(-x)=f(x),且当x>0时,f'(x)>0,则当x<0时,f'(x)<0,是个真命题,由对于任意实数x,有f(-x)=f(x),知此函数是一个偶函数,x>0时,f'(x)>0,知函数在(0,+∞)上是增函数,故在(-∞,0)上是减函数,所以有x<0时,f'(x)<0,
综上证明知①③④是真命题
故答案为:①③④
点评:本题考查命题真假判断与应用,解题的关键是熟练掌握每个命题所涉及的基础知识与基本技能,本题中②③两个命题的真假判断是个难点,其中②的判断用到了特殊值法,③的判断技巧性较强,解题时对此类技巧要注意掌握

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 为两两不重合的平面,
为两两不重合的平面, 为两两不重合的直线,给出下列四个命题:
为两两不重合的直线,给出下列四个命题: ,
, ,则
,则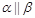 ;
; ,
, ,
, ,
, ,则
,则 ;
;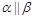 ,
, ,则
,则 ;
; ,
, ,
, ,
, ,则
,则 其中真命
其中真命