题目内容
若存在实数x∈[1，2]满足
，则实数a的取值范围是________．
（-∞，5）
分析：可化为：
，根据对勾函数的单调性，可求出此时不等式右边的范围，进而得到实数a的取值范围
解答：可化为：
当x∈[1，2]时，对勾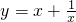函数
为增函数
故
∈[4，5]
若存在实数x∈[1，2]满足，
则a小于的最大值即
∴a＜5
故实数a的取值范围是（-∞，5）
故答案为：（-∞，5）
点评：本题考查的知识点是函数单调性的性质，存在性问题，其中将存在性问题转化为最值问题是解答的关键．
分析：
可化为：，根据对勾函数的单调性，可求出此时不等式右边的范围，进而得到实数a的取值范围解答：
可化为：当x∈[1，2]时，对勾函数
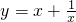为增函数故
∈[4，5]若存在实数x∈[1，2]满足
，则a小于
的最大值即∴a＜5
故实数a的取值范围是（-∞，5）
故答案为：（-∞，5）
点评：本题考查的知识点是函数单调性的性质，存在性问题，其中将存在性问题转化为最值问题是解答的关键．
练习册系列答案
相关题目
