题目内容
设 表示三条不同的直线,
表示三条不同的直线,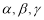 表示三个不同的平面,给出下列四个命题:
表示三个不同的平面,给出下列四个命题:
①若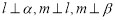 ,则
,则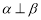 ;
;
②若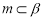 ,
,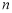 是
是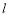 在
在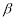 内的射影,
内的射影,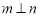 ,则
,则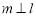 ;
;
③若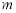 是平面
是平面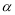 的一条斜线,
的一条斜线,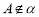 ,
,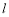 为过
为过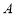 的一条动直线,则可能有
的一条动直线,则可能有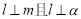 ;
;
④若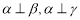 ,则
,则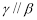
其中真命题的个数为( )个
(A)1 (B)2 (C)3 (D)4
B
【解析】
试题分析: ,则
,则 或
或 ;若
;若 ,则由
,则由 可得
可得 。若
。若 ,则存在
,则存在 有m∥n。因为
有m∥n。因为 ,所以
,所以 ,从而可得
,从而可得 ,①正确;
,①正确;
过l上一点 作
作 ,则B点在直线n上,且AB⊥m。因为n是l在
,则B点在直线n上,且AB⊥m。因为n是l在 上射影,所以l,n平行或相交,从而可得l,n,AB共面。因为m⊥n,所以m⊥l,n,AB所在平面,从而可得m⊥l,②正确;
上射影,所以l,n平行或相交,从而可得l,n,AB共面。因为m⊥n,所以m⊥l,n,AB所在平面,从而可得m⊥l,②正确;
若 ,设
,设 ,则直线AB是直线m在平面α内的射影。因为m是平面α的斜线,所以l,m,AB共面且直线m与直线AB相交。若
,则直线AB是直线m在平面α内的射影。因为m是平面α的斜线,所以l,m,AB共面且直线m与直线AB相交。若 ,由
,由 可得m∥AB,矛盾,③不正确;
可得m∥AB,矛盾,③不正确;
垂直于同一平面的两个平面可能平行或相交,④不正确。
综上可得,选B
考点:本题考查空间线面关系,面面关系,线线关系
点评:解决本题的关键是掌握空间的线面位置关系

练习册系列答案
相关题目
 ,函数
,函数
 的单调递减区间.
的单调递减区间. 的图象向左平移
的图象向左平移 个单位,再将所得图象上各点的横坐标缩短为原来的
个单位,再将所得图象上各点的横坐标缩短为原来的 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数 的图象.求
的图象.求 在
在
 上的值域.
上的值域. 与双曲线
与双曲线 的公共焦点为F1,F2,点P是两条曲线的一个公共点,则cos∠F1PF2的值为 .
的公共焦点为F1,F2,点P是两条曲线的一个公共点,则cos∠F1PF2的值为 . 的一条渐近线方程是 ( )
的一条渐近线方程是 ( ) B.
B. C.
C. D.
D.
 中,
中,  为其前
为其前 项和
项和 ,且
,且
 ,求数列
,求数列 的前
的前 项和
项和 .
.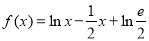 ,
,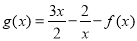 .
.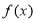 的单调区间;
的单调区间; ,若存在
,若存在 ,对任意的
,对任意的 ,总有
,总有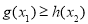 成立,求实数
成立,求实数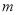 的取值范围.
的取值范围.