题目内容
已知向量 ,函数
,函数
(1)求函数 的单调递减区间.
的单调递减区间.
(2)将函数 的图象向左平移
的图象向左平移 个单位,再将所得图象上各点的横坐标缩短为原来的
个单位,再将所得图象上各点的横坐标缩短为原来的 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数 的图象.求
的图象.求 在
在
 上的值域.
上的值域.
(1) ;(2)
;(2)
【解析】
试题分析:(1)∵
令 ,解得
,解得
所以,减区间为 .
.
(2)因为将函数f(x)向左平移 ,得到
,得到 ,横坐标缩短为原来的
,横坐标缩短为原来的 倍,纵坐标不变,
倍,纵坐标不变,
得到 ,
,
∵ ,∴
,∴ ,∴
,∴ ,
,
∴ ,
,
所以值域为
考点:本题考查平面向量与三角函数的综合,两角和与差的三角函数,函数 的图象和性质
的图象和性质

练习册系列答案
相关题目
从某高中随机选取5名高三男生,其身高和体重的数据如下表所示:
身高 | 160 | 165 | 170 | 175 | 180 |
体重y(kg) | 63 | 66 | 70 | 72 | 74 |
根据上表可得回归直线方程 ,据此模型预报身高为172 cm的高三男生的体重为( )
,据此模型预报身高为172 cm的高三男生的体重为( )
A.70.09 B.70.12 C.70.55 D.71.05
 经过第一、第二和第四象限,则
经过第一、第二和第四象限,则 应满足( )
应满足( ) B.
B. C.
C. D.
D.
 (cm)
(cm)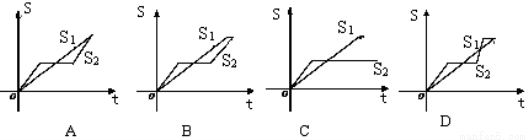
 图象的是( )
图象的是( )
 ,n∈Z,则f (1)+ f (2)+ f (3)+……+f (2012)=_____ _____________
,n∈Z,则f (1)+ f (2)+ f (3)+……+f (2012)=_____ _____________ ,
, ,
, ( )
( ) B.
B. C.
C. D.
D.
 表示三条不同的直线,
表示三条不同的直线,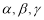 表示三个不同的平面,给出下列四个命题:
表示三个不同的平面,给出下列四个命题: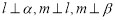 ,则
,则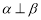 ;
;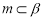 ,
,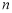 是
是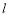 在
在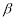 内的射影,
内的射影,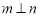 ,则
,则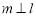 ;
;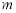 是平面
是平面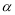 的一条斜线,
的一条斜线,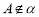 ,
,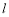 为过
为过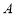 的一条动直线,则可能有
的一条动直线,则可能有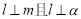 ;
;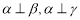 ,则
,则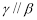
 时,
时, ,则
,则 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.