题目内容
在△ABC中，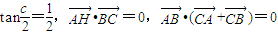
，H在BC边上，则过点B以A、H为两焦点的双曲线的离心率为（ ）A．
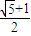
B．
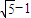
C．
D．
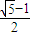
【答案】分析：由已知中在△ABC中，
，H在BC边上，我们根据向量垂直的数量积为0，及二倍角的正切公式，易得△ABC是一个顶角正切为
的等腰三角形，AH为腰上高，由此设出各边的长度，然后根据双曲线的性质及双曲线离心率的定义，即可求出答案．
解答：解：由已知中
可得：AH为BC边上的高
又由
可得：CA=CB
又由
，可得tanC=
令AH=4X，则CH=3X，AC=BC=5X，BH=2X，AB=2
X
则过点B以A、H为两焦点的双曲线中
2a=2（
-1）x，2c=4x
则过点B以A、H为两焦点的双曲线的离心率e=
=
=
故选A
点评：本题考查的知识点是双曲线的简单性质，其中根据已知求出满足条件的△ABC的形状进而求出各边长是解答本题的关键．
，H在BC边上，我们根据向量垂直的数量积为0，及二倍角的正切公式，易得△ABC是一个顶角正切为的等腰三角形，AH为腰上高，由此设出各边的长度，然后根据双曲线的性质及双曲线离心率的定义，即可求出答案．解答：解：由已知中
可得：AH为BC边上的高又由
可得：CA=CB又由
，可得tanC=令AH=4X，则CH=3X，AC=BC=5X，BH=2X，AB=2
X则过点B以A、H为两焦点的双曲线中
2a=2（
-1）x，2c=4x则过点B以A、H为两焦点的双曲线的离心率e=
==故选A
点评：本题考查的知识点是双曲线的简单性质，其中根据已知求出满足条件的△ABC的形状进而求出各边长是解答本题的关键．
练习册系列答案
科学实验活动册系列答案
相关题目
，H在BC边上，则过点B以A、H为两焦点的双曲线的离心率为
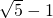
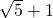
如图，在△ABC中，已知A（-3，0），B（3，0），CD⊥AB于D，△ABC的垂心为
．
能否成等差数列？请说明理由；
，H在BC边上，则过点B以A、H为两焦点的双曲线的离心率为________．
，H在BC边上，则过点B以A、H为两焦点的双曲线的离心率为 ．