题目内容
在直接坐标系xOy中,直线L的方程为x-y+4=0,曲线C的参数方程为 .
.
(1)已知在极坐标(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为(4, ),判断点P与直线L的位置关系;
),判断点P与直线L的位置关系;
(2)设点Q是曲线C上的一个动点,求它到直线l的距离的最小值.
【答案】
(1)点 在直线
在直线 上(2)当
上(2)当 时,
时, 取得最小值,且最小值为
取得最小值,且最小值为
【解析】
试题分析:(1)把极坐标系下的点 化为之间坐标系,得
化为之间坐标系,得
因为点 的直角坐标
的直角坐标 满足直线
满足直线 的方程
的方程 ,所以点
,所以点 在直线
在直线 上.
上.
(2)因为点 在曲线
在曲线 上 ,故可设点
上 ,故可设点 的坐标为
的坐标为 ,从而点
,从而点 到直线
到直线 的距离为
的距离为

由此的,当 时,
时, 取得最小值,且最小值为
取得最小值,且最小值为
考点:极坐标系,点到直线的距离
点评:主要是考查极坐标方程与参数方程的运用,求解点与直线的位置关系,以及最值问题,属于基础题。

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
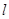 的方程为x-y+4=0,曲线C的参数方程为
的方程为x-y+4=0,曲线C的参数方程为
 ,判断点P与直线
,判断点P与直线 (α为参数)
(α为参数) ),判断点P与直线l的位置关系;
),判断点P与直线l的位置关系;