题目内容
(本题满分10分)《选修4-4:坐标系与参数方程》
在直接坐标系xOy中,直线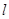 的方程为x-y+4=0,曲线C的参数方程为
的方程为x-y+4=0,曲线C的参数方程为
(1)已知在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为 ,判断点P与直线
,判断点P与直线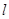 的位置关系;
的位置关系;
(2)设点Q是曲线C上的一个动点,求它到直线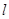 的距离的最小值.
的距离的最小值.
【答案】
(1)点P在直线 上;(2)当
上;(2)当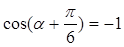 时,d取得最小值,且最小值为
时,d取得最小值,且最小值为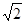 。
。
【解析】
试题分析:(1)由曲线C的参数方程为
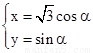 ,知曲线C的普通方程,再由点P的极坐标为(4,
,知曲线C的普通方程,再由点P的极坐标为(4, 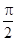 ),知点P的普通坐标为(4cos
),知点P的普通坐标为(4cos 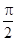 ,4sin
,4sin 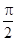 ),即(0,4),由此能判断点P与直线l的位置关系.
),即(0,4),由此能判断点P与直线l的位置关系.
(2)由Q在曲线C: 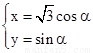 上,(0°≤α<360°),知Q(
上,(0°≤α<360°),知Q( 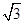 cosα,sinα)到直线l:x-y+4=0的距离d= |2sin(α+θ)+4|,(0°≤α<360°),由此能求出Q到直线l的距离的最小值
cosα,sinα)到直线l:x-y+4=0的距离d= |2sin(α+θ)+4|,(0°≤α<360°),由此能求出Q到直线l的距离的最小值
解:(1)把极坐标系下的点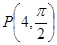 化为直角坐标,得P(0,4)。
化为直角坐标,得P(0,4)。
因为点P的直角坐标(0,4)满足直线 的方程
的方程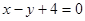 ,
,
所以点P在直线 上,
上,
(2)因为点Q在曲线C上,故可设点Q的坐标为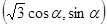 ,
,
从而点Q到直线 的距离为
的距离为
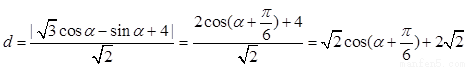
由此得,当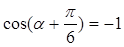 时,d取得最小值,且最小值为
时,d取得最小值,且最小值为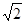
考点:本试题主要考查了椭圆的参数方程和点到直线距离公式的应用,解题时要认真审题,注意参数方程与普通方程的互化,注意三角函数的合理运用.
点评:解决该试题的关键是参数方程与普通方程的互化以及对于点到直线距离公式的灵活运用求解最值。

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
 ,求证:
,求证: ;
; ,求证:三数
,求证:三数 ,
, ,
, 中至少有一个不小于2.
中至少有一个不小于2.
 的所有棱长都为2,
的所有棱长都为2, 为棱
为棱 的中点,
的中点, 平面
平面 ;
; 的余弦值大小.
的余弦值大小.
 与
与 的距离,由于地形的限制,需要在岸上选取
的距离,由于地形的限制,需要在岸上选取 和
和 两点,现测得
两点,现测得 ,
, ,
, ,
, ,
, ,求两景点
,求两景点