题目内容
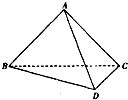 (2009•武汉模拟)如图,在四面体A-BCD中,AB=AD=
(2009•武汉模拟)如图,在四面体A-BCD中,AB=AD=| 2 |
(1)求证:平面ABC上平面BCD;
(2)求直线CD与平面ABC所成角的正弦值.
分析:(1)取BD、BC中点分别为M、N,证明AN和两相交直线BD及MN均垂直,得到AN⊥面BDC,从而证得面ABC⊥面BCD.
(2)由(1)可知平面ABC⊥平面BDC,过D向BC作垂线于足H,从而DH⊥面ABC,解Rt△BDC,求出∠DCH 的正弦值,
即为所求.
(2)由(1)可知平面ABC⊥平面BDC,过D向BC作垂线于足H,从而DH⊥面ABC,解Rt△BDC,求出∠DCH 的正弦值,
即为所求.
解答: 解:(1)证明:在四面体A-BCD中,取BD、BC中点分别为M、N,连接MN,则MN∥DC.
解:(1)证明:在四面体A-BCD中,取BD、BC中点分别为M、N,连接MN,则MN∥DC.
∵BD⊥DC,则MN⊥BD. 又AD=AB=
,则AM⊥BD,∴∠AMN中,AM=1,MN=
,∠AMN=60°,可知∠ANM=90°.
又BD⊥面AMN,则BD⊥AN,∴AN和两相交直线BD及MN均垂直,从而AN⊥面BDC,
又面ABC经过直线AN,故面ABC⊥面BCD.
(2)由(1)可知平面ABC⊥平面BDC,过D向BC作垂线于足H,从而DH⊥面ABC,
在Rt△BDC中,BD=2,DC=1,则DH=
,于是DC与平面ABC所成角即∠DCH,∴sin∠DCH=
=
,
因此直线CD与平面ABC所成角的正弦值为
.
 解:(1)证明:在四面体A-BCD中,取BD、BC中点分别为M、N,连接MN,则MN∥DC.
解:(1)证明:在四面体A-BCD中,取BD、BC中点分别为M、N,连接MN,则MN∥DC.∵BD⊥DC,则MN⊥BD. 又AD=AB=
| 2 |
| 1 |
| 2 |
又BD⊥面AMN,则BD⊥AN,∴AN和两相交直线BD及MN均垂直,从而AN⊥面BDC,
又面ABC经过直线AN,故面ABC⊥面BCD.
(2)由(1)可知平面ABC⊥平面BDC,过D向BC作垂线于足H,从而DH⊥面ABC,
在Rt△BDC中,BD=2,DC=1,则DH=
| 2 | ||
|
| 2 | ||
|
2
| ||
| 5 |
因此直线CD与平面ABC所成角的正弦值为
2
| ||
| 5 |
点评:本题考查证明两个平面垂直的方法,求直线和平面所成的角,体现了数形结合的数学思想,找出直线CD与平面ABC所成角,是解题的关键.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
 (2009•武汉模拟)(文科做) 如图,在边长为a的正方体ABCD-A1B1C1D1中M、N、P、Q分别为AD,CD,BB1,C1D1的中点
(2009•武汉模拟)(文科做) 如图,在边长为a的正方体ABCD-A1B1C1D1中M、N、P、Q分别为AD,CD,BB1,C1D1的中点