题目内容
定义函数 (定义域),若存在常数C,对于任意
(定义域),若存在常数C,对于任意 ,存在唯一的
,存在唯一的 ,使得
,使得 ,则称函数
,则称函数 在D上的“均值”为C.已知
在D上的“均值”为C.已知 ,
, ,则函数
,则函数 在
在 上的均值为( )
上的均值为( )
A.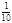 B.
B. C.
C.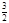 D.10
D.10
C
解析试题分析:根据定义,函数y=f(x),x∈D,若存在常数C,对任意的x1∈D,存在唯一的x2∈D,使得 ,则称函数f(x)在D上的均值为C.
,则称函数f(x)在D上的均值为C.
令x1•x2=10×100=1000
当x1∈[10,100]时,选定x2= ∈[10,100],可得:C=
∈[10,100],可得:C= ,
,
故选C.
考点:新定义问题,对数函数的性质。
点评:中档题,理解题意是解题的关键,利用 ,构造符合题意的x1,x2。
,构造符合题意的x1,x2。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数 是R上的增函数,则
是R上的增函数,则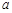 的取值范围是( )
的取值范围是( )
A. ≤ ≤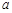 <0 <0 | B. ≤ ≤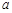 ≤ ≤ | C.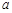 ≤ ≤ | D.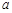 <0 <0 |
已知函数
 ,若|
,若| |≥
|≥ ,则
,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
函数 的图象与
的图象与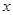 轴所围成的封闭图形的面积为 ( )
轴所围成的封闭图形的面积为 ( )
A. | B.1 | C.4 | D.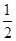 |
下列大小关系正确的是 ( )
A. | B. |
C. | D. |
如果函数f(x)=x +bx+c对于任意实数t,都有f(2+t)=f(2-t),那么( )
+bx+c对于任意实数t,都有f(2+t)=f(2-t),那么( )
| A.f(2)<f(1)<f(4) | B.f(1)<f(2)<f(4) |
| C.f(2)<f(4)<f(1) | D.f(4)<f(2)<f(1) |
如果函数 在区间
在区间 上是减函数,那么实数
上是减函数,那么实数 的取值范围是
的取值范围是
A. | B. | C. | D. |
已知函数 满足
满足 且
且 若对于任意的
若对于任意的 总有
总有 成立,则
成立,则 在
在 内的可能值有( )个
内的可能值有( )个
| A.1 | B.2 | C.3 | D.4 |
 的图像是 ( )
的图像是 ( ) 