题目内容
已知函数 是R上的增函数,则
是R上的增函数,则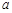 的取值范围是( )
的取值范围是( )
A. ≤ ≤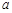 <0 <0 | B. ≤ ≤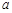 ≤ ≤ | C.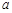 ≤ ≤ | D.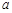 <0 <0 |
B
解析试题分析:函数 是R上的增函数,则
是R上的增函数,则 单调递增,故它的对称轴
单调递增,故它的对称轴 ,即
,即 ,此时
,此时 也单调递增,要保证在R上是增函数,只需在
也单调递增,要保证在R上是增函数,只需在 满足
满足 ,即
,即 ,综上所述
,综上所述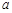 的取值范围是
的取值范围是 .
.
考点:函数的单调性.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设 ,
, (
( ,且
,且 ),若
),若 的图像与
的图像与 的图像有且仅有两个不同的公共点从左向右分别为
的图像有且仅有两个不同的公共点从左向右分别为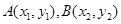 ,则下列判断正确的是( )
,则下列判断正确的是( )
A. 时 时 |
B. 时 时 |
C. 时 时 |
D. 时 时 |
已知函数 ,若
,若 ,则实数
,则实数 等于( )
等于( )
A. | B. | C.2 | D.4 |
已知 ,以下结论中成立的是( )
,以下结论中成立的是( )
A. | B. |
C. | D. |
已知数列 满足
满足 ,且
,且 ,则
,则 的值是( )
的值是( )
A. | B. | C. | D. |
函数 的所有零点之和等于( )
的所有零点之和等于( )
A. | B.2 | C.3 | D.4 |
已知函数 且
且 则
则 的值为( )
的值为( )
A.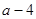 | B. | C. | D.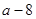 . . |
定义在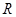 上的函数
上的函数 ,则
,则 ( )
( )
| A.1 | B.2 | C.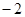 | D. |
 (定义域),若存在常数C,对于任意
(定义域),若存在常数C,对于任意 ,存在唯一的
,存在唯一的 ,使得
,使得 ,则称函数
,则称函数 在D上的“均值”为C.已知
在D上的“均值”为C.已知 ,
, ,则函数
,则函数 上的均值为( )
上的均值为( )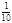 B.
B. C.
C.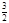 D.10
D.10