题目内容
如果函数 在区间
在区间 上是减函数,那么实数
上是减函数,那么实数 的取值范围是
的取值范围是
A. | B. | C. | D. |
A
解析试题分析:求出函数f(x)=x2+2(a-1)x+2的对称轴x=1-a,令1-a≥4,即可解出a的取值范围.解:函数f(x)=x2+2(a-1)x+2的对称轴x=1-a,又函数在区间(-∞,4]上是减函数,可得1-a≥4,得a≤-3.故选A
考点:二次函数图象的性质
点评:考查二次函数图象的性质,二次项系数为正时,对称轴左边为减函数,右边为增函数,本题主要是训练二次函数的性质.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
定义在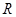 上的函数
上的函数 ,则
,则 ( )
( )
| A.1 | B.2 | C.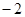 | D. |
下图给出4个幂函数的图像,则图像与函数的大致对应是 
A. | B. |
C. | D. |
设集合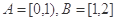 ,函数
,函数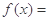


 且
且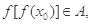
则 的取值范围是 ( )
的取值范围是 ( )
A.( ) ) | B.[0, ] ] | C.( ) ) | D.( ) ) |
已知函数 ,则
,则 的值是 ( )
的值是 ( )
A. | B. | C. | D. |
若函数 ,则
,则 的值是( )
的值是( )
| A.9 | B. | C.-9 | D. |
已知函数 ,若
,若 ,
, ,
, ,则 ( )
,则 ( )
A. | B. | C. | D. |
已知 (
( >0,
>0, >0,
>0, ≠1),
≠1), , 则
, 则 的值为( )
的值为( )
A. | B.  | C.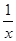 | D. |
 (定义域),若存在常数C,对于任意
(定义域),若存在常数C,对于任意 ,存在唯一的
,存在唯一的 ,使得
,使得 ,则称函数
,则称函数 在D上的“均值”为C.已知
在D上的“均值”为C.已知 ,
, ,则函数
,则函数 上的均值为( )
上的均值为( )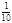 B.
B. C.
C.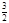 D.10
D.10