Question

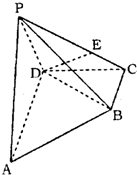（2012•商丘二模）如图，四棱锥P-ABCD中，AD∥BC，AD⊥DC，侧面APD为等腰直角三角形，PA⊥PD，平面PAD⊥底面ABCD，E为侧棱PC上不同于端点的一点．
（Ⅰ）求证：PA⊥DE：
（Ⅱ）设AD=2BC=2，CD=

3

，求三棱锥D-PBC的高．

Answer 1

分析：（Ⅰ）证明PA⊥DE，只需证明PA⊥平面PDC，利用AD⊥DC，平面PAD⊥底面ABCD，可证DC⊥平面PAD，从而可得结论；
（Ⅱ）作PF⊥AD，F为垂足，则F为AD中点，且PF=1，连接BF，可得BC⊥面PFB，作FH⊥PB，垂足为H，由FH?面PFB，可得FH⊥BC，从而FH⊥面PBC，故FH的长度为F到面PBC的距离，即三棱锥D-PBC的高．

解答：（Ⅰ）证明：∵AD⊥DC，平面PAD⊥底面ABCD，平面PAD∩底面ABCD=AD，∴DC⊥平面PAD
∵PA?平面PAD，∴DC⊥PA
∵PA⊥PD，PD∩DC=D，∴PA⊥平面PDC
∵DE?平面PDC，∴PA⊥DE；
（Ⅱ）作PF⊥AD，F为垂足，则F为AD中点，且PF=1，连接BF
∵PF⊥AD，平面PAD⊥底面ABCD，平面PAD∩底面ABCD=AD，∴PF⊥底面ABCD，∴PF⊥BF
∵BC∥FD，BC=FD，∴四边形BCDF是平行四边形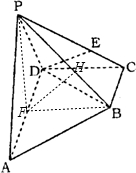
∵BF=CD=

3

，∴PB=2
∵BF∥CD，AD⊥CD，∴AD⊥BF
∵AD⊥PF，BF∩PF=F
∴AD⊥面PFB，∴BC⊥面PFB
作FH⊥PB，垂足为H，由FH?面PFB，可得FH⊥BC
∴FH⊥面PBC，∴FH的长度为F到面PBC的距离
∵FD∥BC，BC?面PBC，FD?面PBC
∴FD∥面PBC
设棱锥D-PBC的高为h，∴h=FH
由PF•FB=PB•FH，得FH=

3

2

∴三棱锥D-PBC的高为

3

2

点评：本题考查面面垂直、线面垂直、线线垂直，考查三棱锥的高，解题的关键是正确面面垂直的性质、线面垂直的判定，正确作出三棱锥的高．