题目内容
若直线 与直线2x+3y-6=0的交点位于第一象限,则直线l的倾斜角的取值范围( )
与直线2x+3y-6=0的交点位于第一象限,则直线l的倾斜角的取值范围( )A.

B.

C.

D.

【答案】分析:联立两直线方程到底一个二元一次方程组,求出方程组的解集即可得到交点的坐标,根据交点在第一象限得到横纵坐标都大于0,联立得到关于k的不等式组,求出不等式组的解集即可得到k的范围,然后根据直线的倾斜角的正切值等于斜率k,根据正切函数图象得到倾斜角的范围.
解答:解:联立两直线方程得: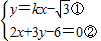 ,
,
将①代入②得:x=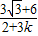 ③,把③代入①,求得y=
③,把③代入①,求得y=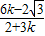 ,
,
所以两直线的交点坐标为(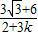 ,
,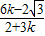 ),
),
因为两直线的交点在第一象限,所以得到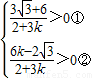 ,
,
由①解得:k>- ;由②解得k>
;由②解得k>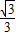 或k<-
或k<- ,所以不等式的解集为:k>
,所以不等式的解集为:k>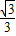 ,
,
设直线l的倾斜角为θ,则tanθ>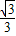 ,所以θ∈(
,所以θ∈(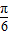 ,
,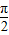 ).
).
故选B.
点评:此题考查学生会根据两直线的方程求出交点的坐标,掌握象限点坐标的特点,掌握直线倾斜角与直线斜率的关系,是一道综合题.
解答:解:联立两直线方程得:
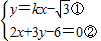 ,
,将①代入②得:x=
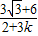 ③,把③代入①,求得y=
③,把③代入①,求得y=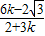 ,
,所以两直线的交点坐标为(
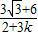 ,
,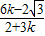 ),
),因为两直线的交点在第一象限,所以得到
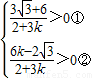 ,
,由①解得:k>-
 ;由②解得k>
;由②解得k>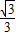 或k<-
或k<- ,所以不等式的解集为:k>
,所以不等式的解集为:k>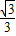 ,
,设直线l的倾斜角为θ,则tanθ>
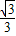 ,所以θ∈(
,所以θ∈(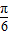 ,
,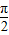 ).
).故选B.
点评:此题考查学生会根据两直线的方程求出交点的坐标,掌握象限点坐标的特点,掌握直线倾斜角与直线斜率的关系,是一道综合题.

练习册系列答案
相关题目
若过点A(-2,m)和B(4,0)的直线与直线2x+y-1=0平行,则m的值为( )
| A、12 | B、-12 | C、3 | D、-3 |