题目内容
已知直线l1过点B(0,-6)且与直线2x-3λy=0平行,直线l2经过定点A(0,6)且斜率为-
,直线l1与l2相交于点P,其中λ∈R,
(1)当λ=1时,求点P的坐标.
(2)试问:是否存在两个定点E、F,使得|PE|+|PF|为定值,若存在,求出E、F的坐标,若不存在,说明理由.
| 2λ | 3 |
(1)当λ=1时,求点P的坐标.
(2)试问:是否存在两个定点E、F,使得|PE|+|PF|为定值,若存在,求出E、F的坐标,若不存在,说明理由.
分析:(1)当λ=1时,根据条件分别写出两直线的方程,联立即可求得点P的坐标.
(2)由条件可得KPB×KPA=-
,由课本椭圆一节的例题可知,点P的轨迹是一个椭圆,求出其方程,再求出其焦点,即选为点E、F,则可满足条件.
(2)由条件可得KPB×KPA=-
| 4 |
| 9 |
解答:解:(1)当λ=1时,直线2x-3λy=0即2x--3y=0,
∵l1与此直线平行,∴可设直线l1的方程为2x-3y+c=0,
又直线l1过点B(0,-6),将其代入得0-3×(-6)+c=0,解得c=-18.∴直线l1的方程为 2x-3y-18=0.
∵直线l2经过定点A(0,6)且斜率为-
,即-
,∴直线l2的方程为y-6=-
x,即2x+3y-18=0.
联立
解得
.即点P(9,0).
(2)∵直线l1与直线2x-3λy=0平行,∴当λ≠0时,直线l1的斜率为
,
而直线l2斜率为-
,又
×(-
)=-
.
设点P(x,y),则KPB×KPA=-
,于是
×
=-
(x≠0),化为
+
=1(x≠0).
当λ=0时,直线l1即为y轴,直线l2即为y=6,
∴二直线交于点(0,6),
∴点P的轨迹为椭圆
+
=1(去掉点(0,-6)).
综上可知:取点E(3
,0),F(-3
,0),则满足|PE|+|PF|为定值.
∵l1与此直线平行,∴可设直线l1的方程为2x-3y+c=0,
又直线l1过点B(0,-6),将其代入得0-3×(-6)+c=0,解得c=-18.∴直线l1的方程为 2x-3y-18=0.
∵直线l2经过定点A(0,6)且斜率为-
| 2λ |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
联立
|
|
(2)∵直线l1与直线2x-3λy=0平行,∴当λ≠0时,直线l1的斜率为
| 2 |
| 3λ |
而直线l2斜率为-
| 2λ |
| 3 |
| 2 |
| 3λ |
| 2λ |
| 3 |
| 4 |
| 9 |
设点P(x,y),则KPB×KPA=-
| 4 |
| 9 |
| y+6 |
| x |
| y-6 |
| x |
| 4 |
| 9 |
| x2 |
| 81 |
| y2 |
| 36 |
当λ=0时,直线l1即为y轴,直线l2即为y=6,
∴二直线交于点(0,6),
∴点P的轨迹为椭圆
| x2 |
| 81 |
| y2 |
| 36 |
综上可知:取点E(3
| 5 |
| 5 |
点评:本题考查了直线与直线平行及相交以及椭圆的定义,理解和掌握以上知识与解题方法是解此题的关键.

练习册系列答案
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
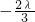 ,直线l1与l2相交于点P,其中λ∈R,
,直线l1与l2相交于点P,其中λ∈R,