题目内容
在△ABC中,D为BC边上一点,DC=2BD,AD=
,∠ADC=60°,若 AC=
AB,则BD等于( )
| 2 |
| 2 |
A、2+
| ||||
B、2+
| ||||
C、
| ||||
D、1+
|
分析:利用余弦定理,结合AC=
AB,即可求出BD.
| 2 |
解答:解:设BD=x,则DC=2x,
由余弦定理可得AB=
,AC=
,
∵AC=
AB,
∴4x2+2-2
x=2(x2+2+
x),
∴x2-2
x-1=0,
解得:x=
+
.
故选:C.
由余弦定理可得AB=
x2+2+
|
4x2+2-2
|
∵AC=
| 2 |
∴4x2+2-2
| 2 |
| 2 |
∴x2-2
| 2 |
解得:x=
| 2 |
| 3 |
故选:C.
点评:本题考查解三角形的实际应用,考查余弦定理,考查学生的计算能力,属于中档题.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
在△ABC中,D为BC的中点,已知
=
,
=
,则下列向量一定与
同向的是( )
| AB |
| a |
| AC |
| b |
| AD |
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
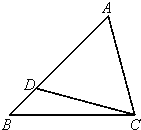 如图,在△ABC中,D为边AB上一点,DA=DC.已知B=
如图,在△ABC中,D为边AB上一点,DA=DC.已知B=