题目内容
在数列{an}中,a1=3,an=-an-1-2n+1(n≥2且n∈N*).(1)求a2,a3的值;
(2)证明:数列{an+n}是等比数列,并求{an}的通项公式;
(3)求数列{an}的前n项和Sn.
【答案】分析:(1)根据a1=3,an=-an-1-2n+1(n≥2且n∈N*),对n进行赋值,可求出a2,a3的值;
(2)直接利用等比数列的定义进行证明,然后利用等比数列性质求其通项公式即可;
(3)先求出数列{an}的通项公式,然后利用分组求和法进行求和即可.
解答:解:(1)∵a1=3,an=-an-1-2n+1(n≥2,n∈N*),
∴a2=-a1-4+1=-6,a3=-a2-6+1=1.
(2)∵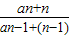 =
=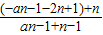 =
=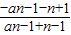 =-1,
=-1,
∴数列{an+n}是首项为a1+1=4,公比为-1的等比数列.
∴an+n=4•(-1)n-1,即an=4•(-1)n-1-n,
∴{an}的通项公式为an=4•(-1)n-1-n(n∈N*).
(3)∵{an}的通项公式为an=4•(-1)n-1-n(n∈N*),
所以Sn=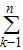 ak=
ak=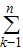 [4•(-1)k-1-k]=
[4•(-1)k-1-k]=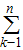 [4•(-1)k-1-
[4•(-1)k-1-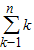
=4×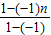 -
-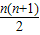
=2[1-(-1)n]- (n2+n)
(n2+n)
=-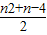 -2(-1)n.
-2(-1)n.
点评:本题主要考查了数列的通项公式,以及等比数列的判定和数列的求和,同时考查了运算求解的能力,属于中档题.
(2)直接利用等比数列的定义进行证明,然后利用等比数列性质求其通项公式即可;
(3)先求出数列{an}的通项公式,然后利用分组求和法进行求和即可.
解答:解:(1)∵a1=3,an=-an-1-2n+1(n≥2,n∈N*),
∴a2=-a1-4+1=-6,a3=-a2-6+1=1.
(2)∵
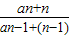 =
=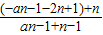 =
=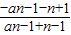 =-1,
=-1,∴数列{an+n}是首项为a1+1=4,公比为-1的等比数列.
∴an+n=4•(-1)n-1,即an=4•(-1)n-1-n,
∴{an}的通项公式为an=4•(-1)n-1-n(n∈N*).
(3)∵{an}的通项公式为an=4•(-1)n-1-n(n∈N*),
所以Sn=
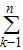 ak=
ak=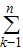 [4•(-1)k-1-k]=
[4•(-1)k-1-k]=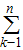 [4•(-1)k-1-
[4•(-1)k-1-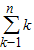
=4×
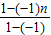 -
-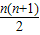
=2[1-(-1)n]-
 (n2+n)
(n2+n)=-
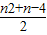 -2(-1)n.
-2(-1)n.点评:本题主要考查了数列的通项公式,以及等比数列的判定和数列的求和,同时考查了运算求解的能力,属于中档题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 ,并且对任意n∈N*,n≥2都有an•an-1=an-1-an成立,令bn=
,并且对任意n∈N*,n≥2都有an•an-1=an-1-an成立,令bn= (n∈N*).
(n∈N*). }的前n项和为Tn,证明:
}的前n项和为Tn,证明: .
.