题目内容
进行某种试验,设试验成功的概率为
,失败的概率为
,以ξ表示试验首次成功所需试验的次数,试写出ξ的分布列,并计算ξ取偶数的概率.
分析：本题考查如何布列离散型随机变量的分布列,以及如何求它的和的概率.其中ξ=k表示前(k-1)次试验失败而第k次试验成功这一事件,ξ服从几何分布.它是相互独立事件同时发生的概率模型.设事件A1,A2,…,An相互独立,那么这n个事件同时发生的概率等于每个事件发生的概率的积,即P(A1·A2·…·An)=P(A1)·P(A2)·…·P(An).
解：随机变量ξ的取值是1,2,3,…,k,….
∵P(ξ=1)=,
P(ξ=2)=·(
),
P(ξ=3)=
·(
)2,
…
P(ξ=k)=
·(
)k-1,
…
ξ | 1 | 2 | 3 | … | K | … |
P |
|
|
| … |
| … |
·
·（
）2
·（
）k-1∴ξ的分布列为取偶数的概率为
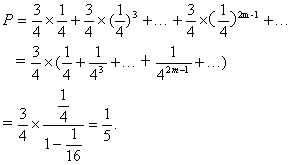
练习册系列答案
学而优衔接教材南京大学出版社系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
，用ξ表示试验首次成功所需试验的次数，则Dξ等于
C.
D. 
为考查某种药物预防疾病的效果,进行动物试验,得到如下丢失数据的列联表:
药物效果试验列联表
|
|
患病 |
未患病 |
总计 |
|
没服用药 |
20 |
30 |
50 |
|
服用药 |
x |
y |
50 |
|
总计 |
M |
N |
100 |
设从没服用药的动物中任取两只,未患病数为X;从服用药物的动物中任取两只,未患病数为Y,工作人员曾计算过P(X=0)=
P(Y=0).
(1)求出列联表中数据x,y,M,N的值;
(2)能够有多大的把握认为药物有效?
(3)现在从该100头动物中,采用随机抽样方法每次抽取1头,抽后返回，抽取5次, 若每次抽取的结果是相互独立的，记被抽取的5头中为服了药还患病的数量为
.,求的期望E()和方差D().
参考公式：
（其中
）
|
P(K2≥k) |
0.25 |
0.15 |
0.10 |
0.05 |
0.010 |
0.005 |
|
k |
1.323 |
2.072 |
2.706 |
3.845 |
6.635 |
7.879 |
，以ξ表示试验首次成功所需试验的次数，试写出ξ的分布列，并写出ξ取偶数的概率（只列出式子）.? 
，失败的概率为
，以
表示首次成功时所需要的试验次数，则E