Question

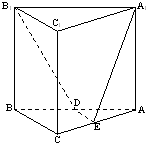（2008•静安区一模）如图，已知直三棱柱ABC-A₁B₁C₁中，∠ACB=90°，∠BAC=30°，BC=1，AA₁=

6

，点D、E分别是△ABC边AB、AC的中点，求：
（1）该直三棱柱的侧面积；
（2）异面直线DE与A₁B₁所成的角的大小．

Answer 1

分析：（1）根据题意求出AC、AB的长，然后利用直三棱柱的侧面展开图是矩形，并且该矩形的长为△ABC的周长，宽为三棱柱的高，即可求得结果；
（2）根据异面直线所成的角的定义，找出异面直线DE与A₁B₁所成的角，然后解三角形即可求得结果．

解答：解：（1）∵，∠ACB=90°，∠BAC=30°，BC=1，
∴AB=2，AC=

3

，
∴S_侧=（AB+AC+BC）AA₁=(3+

3

)

6

；
（2）∵AB∥A₁B₁，
∴∠ADE就是异面直线DE与A₁B₁所成的角，
∵∠ADE=∠ABC=60°，
∴异面直线DE与A₁B₁所成的角为60°．

点评：本题考查柱体的侧面积，一般利用侧面展开图求解，以及异面直线所成的角，平移法是解决异面直线所成的角的注意方法，体现了转化的数学思想方法，属基础题．