题目内容
已知a∈R,求函数f(x)=x2eax的单调区间。
解:函数f(x)的导数:
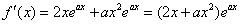
(i)当a=0时,若x<0,则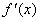 <0,若x>0,则
<0,若x>0,则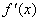 >0
>0
所以当a=0时,函数f(x)在区间(-∞,0)内为减函数,在区间(0,+∞)内为增函数;
(ii)当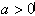 时,由
时,由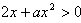 ,解得
,解得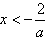 或
或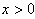
由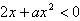 ,解得
,解得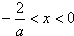
所以,当a>0时,函数f(x)在区间(-∞,-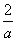 )内为增函数,在区间(-
)内为增函数,在区间(-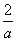 ,0)内为减函数,在区间(0,+∞)内为增函数;
,0)内为减函数,在区间(0,+∞)内为增函数;
(iii)当a<0时,由2x+ax2>0,解得0<x<-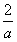 ,由2x+ax2<0,解得x<0或x>-
,由2x+ax2<0,解得x<0或x>-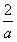
所以当a<0时,函数f(x)在区间(-∞,0)内为减函数,在区间(0,-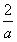 )内为增函数,
)内为增函数,
在区间(-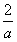 ,+∞)内为减函数。
,+∞)内为减函数。
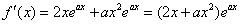
(i)当a=0时,若x<0,则
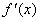 <0,若x>0,则
<0,若x>0,则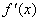 >0
>0所以当a=0时,函数f(x)在区间(-∞,0)内为减函数,在区间(0,+∞)内为增函数;
(ii)当
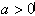 时,由
时,由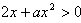 ,解得
,解得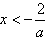 或
或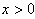
由
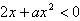 ,解得
,解得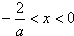
所以,当a>0时,函数f(x)在区间(-∞,-
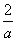 )内为增函数,在区间(-
)内为增函数,在区间(-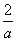 ,0)内为减函数,在区间(0,+∞)内为增函数;
,0)内为减函数,在区间(0,+∞)内为增函数;(iii)当a<0时,由2x+ax2>0,解得0<x<-
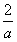 ,由2x+ax2<0,解得x<0或x>-
,由2x+ax2<0,解得x<0或x>-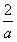
所以当a<0时,函数f(x)在区间(-∞,0)内为减函数,在区间(0,-
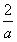 )内为增函数,
)内为增函数,在区间(-
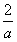 ,+∞)内为减函数。
,+∞)内为减函数。
练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案
相关题目