题目内容
7.一个算法的程序框图如图所示,该程序输出的结果为( )
| A. | $\frac{10}{11}$ | B. | $\frac{36}{55}$ | C. | $\frac{5}{11}$ | D. | $\frac{72}{55}$ |
分析 模拟执行程序框图,可得程序框图的功能是求S=$\frac{1}{1×3}+\frac{1}{2×4}+…+\frac{1}{9×11}$的值,用裂项法即可求值.
解答 解:模拟执行程序框图,可得程序框图的功能是求S=$\frac{1}{1×3}+\frac{1}{2×4}+…+\frac{1}{9×11}$的值,
由S=$\frac{1}{1×3}+\frac{1}{2×4}+…+\frac{1}{9×11}$=$\frac{1}{2}$(1-$\frac{1}{3}$)+$\frac{1}{2}$($\frac{1}{2}-\frac{1}{4}$)+…+$\frac{1}{2}$($\frac{1}{9}-\frac{1}{11}$)=$\frac{1}{2}×$(1+$\frac{1}{2}$+$\frac{1}{3}$..+$\frac{1}{9}$-$\frac{1}{3}$$-\frac{1}{4}$-…-$\frac{1}{11}$)=$\frac{1}{2}×$(1+$\frac{1}{2}$-$\frac{1}{10}$$-\frac{1}{11}$)=$\frac{36}{55}$.
故选:B.
点评 本题主要考查了循环结构的程序框图,考查了裂项法求数列的和,属于基础题.

练习册系列答案
相关题目
15.已知平面向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为120°,$\overrightarrow{a}$=(2,0),|$\overrightarrow{b}$|=1,则|$\overrightarrow{a}$+2$\overrightarrow{b}$|=( )
| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4 | D. | 12 |
16.已知奇函数y=f(x)的导函数f′(x)<0在R恒成立,且x,y满足不等式f(x2-2x)+f(y2-2y)≥0,则$\sqrt{{x^2}+{y^2}}$的取值范围是( )
| A. | $[0,2\sqrt{2}]$ | B. | $[0,\sqrt{2}]$ | C. | [1,2] | D. | $[\sqrt{2},2\sqrt{2}]$ |
11.若关于x的方程ax-x-a=0有两个解,则实数a的取值范围是( )
| A. | (1,+∞) | B. | (0,1) | C. | (0,+∞) | D. | ∅ |


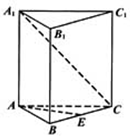 如图,已知正三棱柱ABC-A1B1C1的各棱长均相等,E是BC的中点,点F在侧棱CC1上,且CC1=4CF
如图,已知正三棱柱ABC-A1B1C1的各棱长均相等,E是BC的中点,点F在侧棱CC1上,且CC1=4CF