题目内容
设z1、z2为非零复数,A=z1·
解:设z1=a+bi,z2=c+di(a、b、c、d∈R),?
则A=![]() +
+![]() =(a+bi)(c-di)+(a-bi)(c+di)=2(AC+BD)∈R,?
=(a+bi)(c-di)+(a-bi)(c+di)=2(AC+BD)∈R,?
B=z1·![]() +
+![]() ·z2=a2+b2+c2+d2∈R.?
·z2=a2+b2+c2+d2∈R.?
由于A、B都是实数,所以A、B可以比较大小.又B-A=a2+b2+c2+d2-2(AC+BD)=(a-c)2+(b-d)2≥0,于是得到A≤B,?
当且仅当a=c且b=d,即z1=z2时,取等号.

练习册系列答案
相关题目
 (2004•朝阳区一模)设z1,z2是两个非零复数,且|z1+z2|=|z1-z2|;设复数z=z1+z2,在复平面内与复数z、z1、z2对应的向量分别为
(2004•朝阳区一模)设z1,z2是两个非零复数,且|z1+z2|=|z1-z2|;设复数z=z1+z2,在复平面内与复数z、z1、z2对应的向量分别为
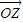 、
、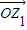 、
、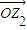 .
.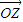 、
、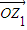 、
、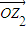 ,并说出以O、Z1、Z、Z2为顶点的四边形的名称;
,并说出以O、Z1、Z、Z2为顶点的四边形的名称;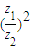 是负实数.
是负实数.