题目内容
设z1，z2是两个非零复数，且|z1+z2|=|z1-z2|；设复数z=z1+z2，在复平面内与复数z、z1、z2对应的向量分别为
、
、
．
（Ⅰ）在复平面内画出向量
、
、
，并说出以O、Z1、Z、Z2为顶点的四边形的名称；
（Ⅱ）求证：(
)2是负实数．
| OZ |
| OZ1 |
| OZ2 |
（Ⅰ）在复平面内画出向量
| OZ |
| OZ1 |
| OZ2 |
（Ⅱ）求证：(
| z1 |
| z2 |
（Ⅰ）图形如图，
所画图形是矩形．
（Ⅱ）证明：由|z1+z2|=|z1-z2|，∵z1、z2不等于零，得|
+1|=|
-1|，
它表示复数
在复平面上对应的点，到点（-1，0），（1，0）的距离相等，
∴
对应的点是复平面虚轴上的点．
∴
是纯虚数．
∴(
)2是负实数．
所画图形是矩形．
（Ⅱ）证明：由|z1+z2|=|z1-z2|，∵z1、z2不等于零，得|
| z1 |
| z2 |
| z1 |
| z2 |
它表示复数
| z1 |
| z2 |
∴
| z1 |
| z2 |
∴
| z1 |
| z2 |
∴(
| z1 |
| z2 |
练习册系列答案
阅读快车系列答案
相关题目
（2004•朝阳区一模）设z1，z2是两个非零复数，且|z1+z2|=|z1-z2|；设复数z=z1+z2，在复平面内与复数z、z1、z2对应的向量分别为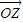
、
、
．
、
、
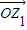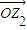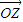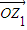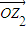，并说出以O、Z1、Z、Z2为顶点的四边形的名称；
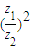是负实数．