Question

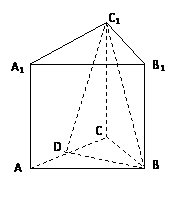
（08年中卫一中三模理）（12分）  如图，三棱柱ABC―A₁B₁C₁中，AA₁⊥面ABC，BC⊥AC，BC=AC=2，AA₁=3，D为AC的中点.

   （Ⅰ）求证：AB₁ // 面BDC₁；

 （Ⅱ）求二面角C₁―BD―C的余弦值；

   （Ⅲ）在侧棱AA­₁上是否存在点P，使得CP⊥面BDC₁？并证明你的结论.

 

Answer 1

解析：（1）连接B₁C，交BC₁于点O，则O为B₁C的中点，

        ∵D为AC中点    ∴OD∥B₁A

        又B₁A平面BDC₁，OD平面BDC₁

         ∴B₁A∥平面BDC₁

  （2）∵AA₁⊥面ABC，BC⊥AC，AA₁∥CC₁

       ∴CC₁⊥面ABC

      则BC⊥平面AC₁，CC₁⊥AC

      如图以C为坐标原点，CA所在直线为X轴，CB所在直线为Y轴，所在直线为轴建立空间直角坐标系 则C₁(0,0,3) B(0,2,0) D(1,0,0) C(0,0,0)

      ∴

      设平面的法向量为

      则

      又平面BDC的法向量为

      ∴二面角C₁―BD―C的余弦值：cos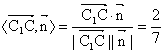

（Ⅲ）设P(h,2,0)   则

若CP⊥面BDC₁   则∥   即（2,0, h）=λ(2,-6,3)

此时λ不存在

∴在侧棱AA­₁上不存在点P，使得CP⊥面BDC₁