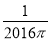题目内容
3.存在函数f(x)满足:对任意x∈R都有( )| A. | f(|x|)=x | B. | f(|x|)=x2+2x | C. | f(|x+1|)=x | D. | f(|x+1|)=x2+2x |
分析 在A、B中,分别取x=±1,由函数性质能排除选项A和B;令|x+1|=t,t≥0,则x2+2x=t2-1,求出f(x)=x2-1,能排除选项C.
解答 解:在A中,取x=1,则f(1)=1,取x=-1,则f(1)=-1,不成立;
在B中,令|x|=t,t≥0,x=±t,取x=1,则f(1)=3,取x=-1,则f(1)=-1,不成立;
在C中,令|x+1|=t,t≥0,则x2+2x=t2-1,
∴f(t)=t2-1,即f(x)=x2-1,故C不成立,D成立.
故选:D.
点评 本题考查抽象函数的性质,是中档题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
相关题目
8.若向量$\overrightarrow a=(\sqrt{2}cosα,\sqrt{2}sinα)$,$\overrightarrow b=(2cosβ,2sinβ)$,且$\frac{π}{6}≤α<\frac{π}{2}<β≤\frac{5π}{6}$,若$\overrightarrow a⊥(\overrightarrow b-\overrightarrow a)$,则β-α的值为( )
| A. | $\frac{π}{4}$或$\frac{3π}{4}$ | B. | $\frac{π}{4}$ | C. | $\frac{3π}{4}$ | D. | $\frac{π}{4}$或$\frac{7π}{4}$ |
15.在空间坐标系O-xyz中,已知点A(2,1,0),则与点A关于原点对称的点B的坐标为( )
| A. | (2,0,1) | B. | (-2,-1,0) | C. | (2,0,-1) | D. | (2,-1,0) |
13.下列函数中,导数不等于$\frac{1}{2}$sin2x的是( )
| A. | 2-$\frac{1}{4}$cos2x | B. | 2+$\frac{1}{2}$sin2x | C. | $\frac{1}{2}$sin2x | D. | x-$\frac{1}{2}$cos2x |
 ,则
,则 的值为( )
的值为( ) B.1 C.
B.1 C. D.
D.
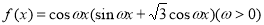 ,如果存在实数
,如果存在实数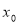 ,使得对任意的实数
,使得对任意的实数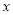 ,都有
,都有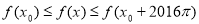 成立,则
成立,则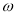 的最小值为( )
的最小值为( )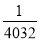 B.
B.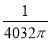 C.
C. D.
D.