题目内容
在△ABC中,设
=
,求A的值.
| tanA |
| tanB |
| 2c-b |
| b |
∵
=
,
根据正弦定理得
=
∴sinAcosB+sinBcosA=2sinCcosA
∴sin(A+B)=2sinCcosA
∴sinC=2sinCcosA
∴cosA=
∴A=60°
| tanA |
| tanB |
| 2c-b |
| b |
根据正弦定理得
| sinAcosB |
| sinBcosA |
| 2sinC-sinB |
| sinB |
∴sinAcosB+sinBcosA=2sinCcosA
∴sin(A+B)=2sinCcosA
∴sinC=2sinCcosA
∴cosA=
| 1 |
| 2 |
∴A=60°

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目
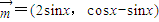 ,
,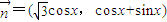 ,函数
,函数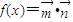 .
.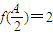 且a2=bc,试判断△ABC的形状.
且a2=bc,试判断△ABC的形状.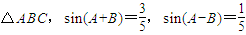 .
.