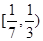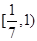题目内容
已知函数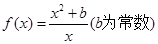 .
.
(Ⅰ)当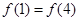 ,函数
,函数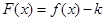 有且仅有一个零点
有且仅有一个零点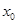 ,且
,且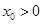 时,求
时,求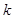 的值;
的值;
(Ⅱ)若函数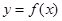 在区间
在区间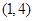 上为单调函数,求
上为单调函数,求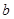 的取值范围.
的取值范围.
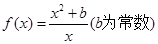 .
.(Ⅰ)当
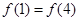 ,函数
,函数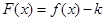 有且仅有一个零点
有且仅有一个零点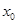 ,且
,且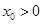 时,求
时,求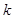 的值;
的值;(Ⅱ)若函数
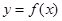 在区间
在区间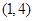 上为单调函数,求
上为单调函数,求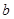 的取值范围.
的取值范围.(1) ;(2)
;(2) 或
或 .
.
 ;(2)
;(2) 或
或 .
.试题分析:(1)由
 可求出
可求出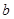 的值,然后将
的值,然后将 有且仅有一个零点
有且仅有一个零点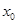 ,且
,且 ,转化函数
,转化函数 的图像与直线
的图像与直线 有且只有一个交点,最后根据图像可得出
有且只有一个交点,最后根据图像可得出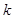 的值;(2)针对
的值;(2)针对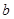 进行分类:
进行分类: 、
、 、
、 并结合双勾函数的单调性可求得
并结合双勾函数的单调性可求得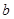 的取值范围.
的取值范围.试题解析:(Ⅰ)

 ,得
,得 , 3分
, 3分 ,作出该函数的图像
,作出该函数的图像
 函数
函数 有且仅有一个零点
有且仅有一个零点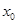 ,且
,且
 由图像可知,函数
由图像可知,函数 的图像与直线
的图像与直线 有且只有一个交点,且交点的横坐标为
有且只有一个交点,且交点的横坐标为 6分
6分 8分
8分(Ⅱ)若
 ,则函数
,则函数 在区间
在区间 上单调递增,满足题意;
上单调递增,满足题意;若
 ,则
,则 ,也满足题意; 10分
,也满足题意; 10分若
 ,则函数
,则函数 在区间
在区间 上单调递减,在区间
上单调递减,在区间 上单调递增,则要满足函数
上单调递增,则要满足函数 在区间
在区间 上为单调函数,则
上为单调函数,则 或
或 ,
,得
 或
或 14分
14分所以,综上所述,得,
 的取值范围是
的取值范围是 或
或 16分.
16分.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 是
是 上的奇函数,且
上的奇函数,且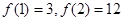
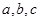 的值
的值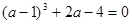 ,
,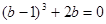 ,求
,求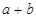 的值
的值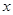 的不等式
的不等式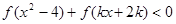 在
在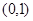 上恒成立,求
上恒成立,求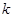 的取值范围
的取值范围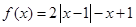 .
.
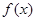 的图像;
的图像;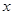 的方程
的方程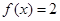 在区间
在区间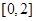 上解的个数.
上解的个数.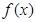 中,满足“对任意的
中,满足“对任意的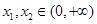 时,均有
时,均有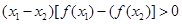 ”的是( )
”的是( )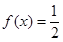
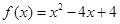
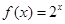
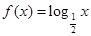
 是定义在R上的偶函数,且在
是定义在R上的偶函数,且在 上是增函数,则一定有( )
上是增函数,则一定有( )
 ≥
≥

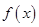 在(6, +∞)上为减函数,且函数y=f(x+6)为偶函数,则( )
在(6, +∞)上为减函数,且函数y=f(x+6)为偶函数,则( )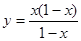
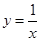
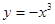
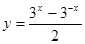
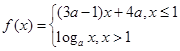 是
是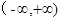 上的减函数,那么实数
上的减函数,那么实数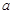 的取值范围是( )
的取值范围是( )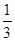 )
)