题目内容
AB是抛物线y2=x的一条焦点弦,若|AB|=4,则AB的中点到直线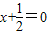 的距离为 .
的距离为 .
【答案】分析:先根据抛物线的方程求得抛物线的准线方程,进而根据抛物线的定义求得AB的中点到准线的距离,根据直线 与准线的距离进而求得AB的中点到直线
与准线的距离进而求得AB的中点到直线 的距离.
的距离.
解答:解:根据抛物线方程可知抛物线准线方程为x=-
则AB的中点到准线的距离= =2
=2
∴AB的中点到直线 的距离为2+
的距离为2+ =
=
故答案为:
点评:本题主要考查了抛物线的简单性质.涉及抛物线的焦点弦的问题常需用抛物线的定义来解决.
 与准线的距离进而求得AB的中点到直线
与准线的距离进而求得AB的中点到直线 的距离.
的距离.解答:解:根据抛物线方程可知抛物线准线方程为x=-

则AB的中点到准线的距离=
 =2
=2∴AB的中点到直线
 的距离为2+
的距离为2+ =
=
故答案为:

点评:本题主要考查了抛物线的简单性质.涉及抛物线的焦点弦的问题常需用抛物线的定义来解决.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案
相关题目