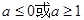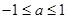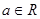题目内容
函数f(x)= +
+ -3x—4在[0,2]上的最小值是
-3x—4在[0,2]上的最小值是
A.— | B.—  | C.-4 | D.—1 |
A
解析试题分析: ,令
,令 得:
得: ,求得
,求得
极值 ,函数值
,函数值 ,所以,函数在[0,2]上的最小值为—
,所以,函数在[0,2]上的最小值为— 。故选A。
。故选A。
考点:利用导数求闭区间上函数的最值.
点评:本题以函数为载体,考查利用导数求闭区间上函数的最值,解题的关键是利用导数确定函数的单调性.

练习册系列答案
相关题目
设 ,若f(3)="3f" ′(x0),则x0=( )
,若f(3)="3f" ′(x0),则x0=( )
| A.±1 | B.±2 | C.± | D.2 |
对于实数集 上的可导函数
上的可导函数 ,若满足
,若满足 ,则在区间[1,2]上必有( )
,则在区间[1,2]上必有( )
A. |
B. |
C. |
D. 或 或 |
已知函数 则下列结论正确的( )
则下列结论正确的( )
A. 在 在 上恰有一个零点 上恰有一个零点 |
B. 在 在 上恰有两个零点 上恰有两个零点 |
C. 在 在 上恰有一个零点 上恰有一个零点 |
D. 在 在 上恰有两个零点 上恰有两个零点 |
设曲线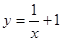 在点(1,2)处的切线与直线
在点(1,2)处的切线与直线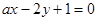 平行,则
平行,则 =( )
=( )
| A.-1 | B.0 | C.-2 | D.2 |
设函数 ,(
,( 是互不相等的常数),则
是互不相等的常数),则 等于( )
等于( )
A. | B. | C. | D. |
若曲线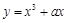 在坐标原点处的切线方程是
在坐标原点处的切线方程是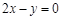 ,则实数
,则实数 ( )
( )
| A.1 | B.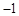 | C.2 | D.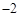 |
曲线 在
在 处的切线的倾斜角是( )
处的切线的倾斜角是( )
A. | B. | C. | D. |
 满足:①当
满足:①当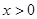 时,
时, 恒成立;②对任意的
恒成立;②对任意的 都有
都有 。又函数
。又函数 满足:对任意的
满足:对任意的 成立,当
成立,当 时,
时, 。若关于
。若关于 的不等式
的不等式 对
对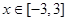 恒成立,则
恒成立,则 的取值范围( )
的取值范围( )